

Bouncing Barney Explored by:
Aubrey D. Johnson
Some how Barney got away from all his friends and ended up in a triangular shaped room. He is trying to get out but can not remember which wall the door is on.
Barney will start on BC and walk parallel to AC.
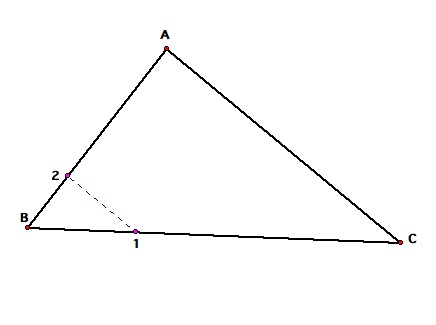
Barney then walks parallel to BC, and the parallel to AB.
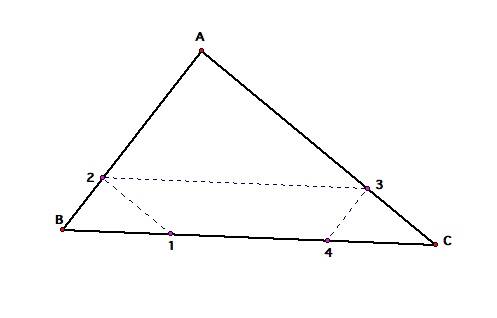
Barney is starting to get frustrated because he can not find a way out. If he continues in this way, how many times total will he hit a wall, before he ends up where he started?
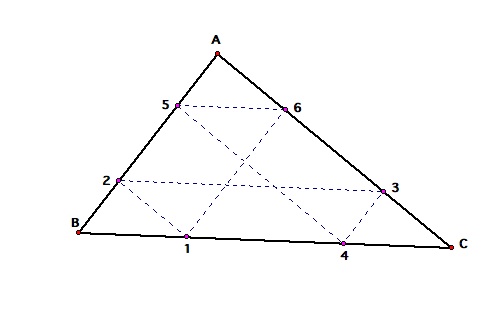
Barney the walls (edges) of the triangle 6 times, it is on the 7th time that he returns to his original starting point. He then notices that the door had been in that space the whole time, and leaves to re join his friends.

Notice that angle 123 = angle 456, and that angle 234 = angle 561.
Now while Barney was going in triangles inside the room his friends were outside trying to find him.
His friends follow this pattern, and wonder where they will end up, and if Barney will be there when they get there.
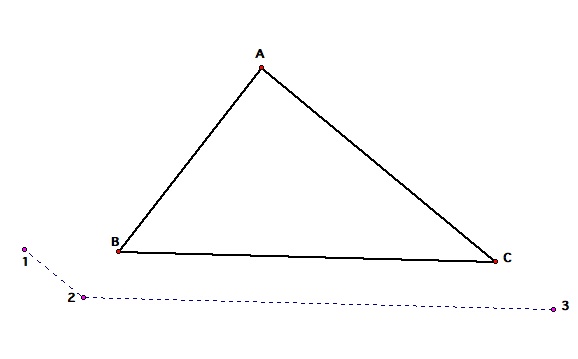
Will they end up where they started like Barney did? Or will they somewhere else?
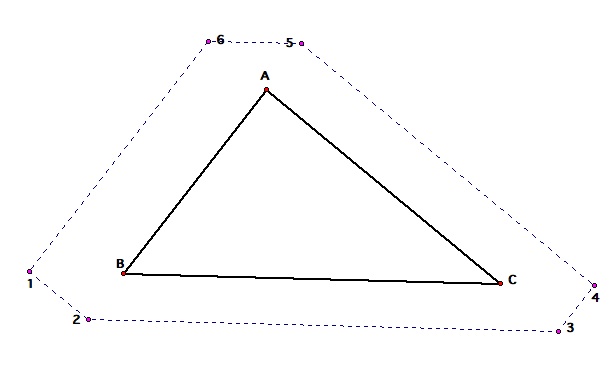
His friends ended up where they started as well. After looking for Barney he came out of the room. And everyone shared their adventures.
Now that they have all shared their stories they all go into the room to see what new mathematical adventures they will have. But, they can not find the door that Barney just came out of...they find themselves inside the room in the center of the back wall.
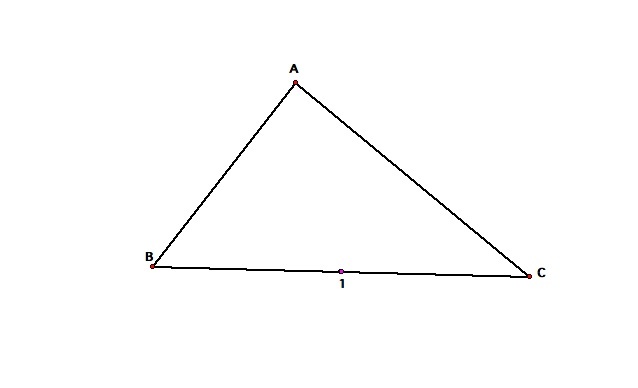
The group wants to see if they will hit the walls 7 times from their starting point, so they follow Barney's instructions and walk parallel to AC.
They find themselves in the center of wall AB, and wonder if they will end up in the center of the opposite wall.
They are amazed that they returned to the starting point on the 4th wall hit. They want to know if their is any significance (mathematically) to what just happened and they found that all four triangles are congruent to each other.
The link above is so that you can play with bouncing Barney and see what other discoveries there are. Move the starting point inside and outside the triangle. Alter the shape and size of the overall triangle.