
Fibonnaci sequence
by
Hee Jung Kim
A Fibonnaci sequence is a recursive sequence with the following rule:
f(0) = 1, f(1) = 1, f(n) = f(n-1) + f(n-2)
Using the spreadsheet we have the following sequence of numbers.

I. When we consider the ratio of two successive terms of the Fibonacci sequence, that is, the ratio of the greater one to the lesser, we have a new sequence, the sequence of ratios of consecutive Fibonacci numbers:
a(0) = 1/1, a(1) = 2/1, a(n) = f(n+1)/f(n)
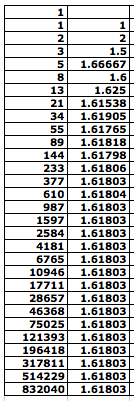
When we assume that a(n) = f(n+1)/f(n) converges to L as n gets bigger and bigger, we have:
a(n) = f(n+1)/f(n) = (f(n)+f(n-1))/f(n) = 1 + f(n-1)/f(n) = 1 + 1/(1/(f(n)/f(n-1)))
As n goes to infinty, L = 1 + 1/L.
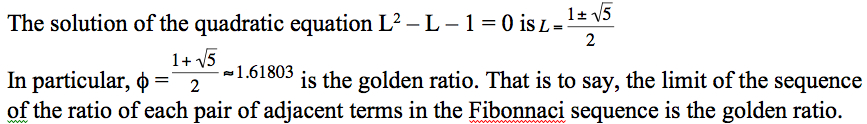
The second column of the spreadsheet above supports that the sequence a(n) of the ratio of the Fibonnaci sequence converges to the golden ratio even though first several values oscillated up and down.
How about the sequence b(n) = f(n+2)/f(n)? To what is it convergent?
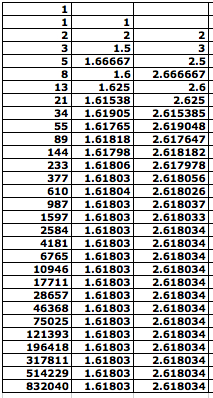
The last column says that the sequence b(n) approaches the golden ratio more than 1. Can we show it?
b(n) = f(n+2)/f(n) = (f(n+1) + f(n))/f(n) = f(n+1)/f(n) + 1
= a(n) + 1
Again, assuming a(n) converges to L, and by
taking the limit both sides as n goes to the infinity, the limit of the
sequence b(n) is L + 1. That is why the last number in the third column
is approximately the last number in the second column more than 1. If we
think the limit of b(n) in relation to the golden ratio, the limit of b(n)
is the golden ratio squared: ![]() . In
fact, because the golden ratio satsfies the quadratic equation above,
. In
fact, because the golden ratio satsfies the quadratic equation above, ![]() .
.
Now, let's observe the sequence c(n) = f(n+3)/f(n)?
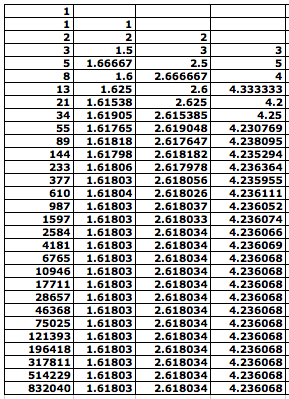
The last column shows part of the sequence
c(n), from which we guess the limit of c(n): approximately 4.236068. What
is it related to the golden ratio ![]() ?
?
c(n) = f(n+3)/f(n) = (f(n+2) + f(n+1))/f(n) = f(n+2)/f(n) + f(n+1)/f(n)
= b(n) + a(n) = a(n) + a(n) + 1 = 2a(n) +1
Therefore the limit, with the same assumption,
of c(n) will be 2L + 1, in other words, 2![]() + 1. This is corresponding to the golden ratio cubed because:
+ 1. This is corresponding to the golden ratio cubed because:
![]()
Lastly, let's observe the sequence d(n) = f(n+4)/f(n) of the ratio.
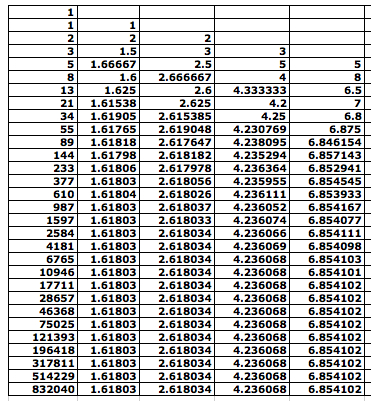
The process is exactly the same as above. We
have that the limit of d(n) is ![]() ,
that is
,
that is ![]() .
.
To sum up, the sequence x(n) = f(n + k)/f(n)
(k = 1, 2, ...) of the ratio of terms of the Fibonnaci sequence f(n) approaches
![]() . Interestingly, both sequence
of the coefficients of
. Interestingly, both sequence
of the coefficients of ![]() and the
sequence of the constants of the limit are the Fibonnaci sequence.
and the
sequence of the constants of the limit are the Fibonnaci sequence.
II. What happens if we change the initial conditions, f(0) = 1 and f(1) = 1 of the Fibonnaci sequence and the sequence of the ratio of terms of it? The spreadsheet is of help to see the difference instantly. Let's use f(0) = 1 and f(1) = 3.
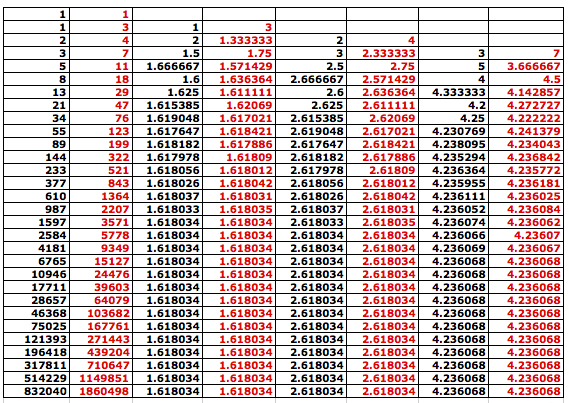
The columns in red are from the 'modified' Fibonnaci sequence. We find that the change from f(1) = 1 to f(1) = 3 did not affect the limit of the sequence of the ratio of terms of the Fibonnaci sequence. It is easy to elicit the result from the process how we got the limit in part I. The initial conditions did not seriously involve in the process of finding the limit of each sequence.
Let's have some other cases for f(1) = a and f(2) = b using the spreadsheets to ensure the argument.
(1) Any intergers (including 0) a and b such that a < b:
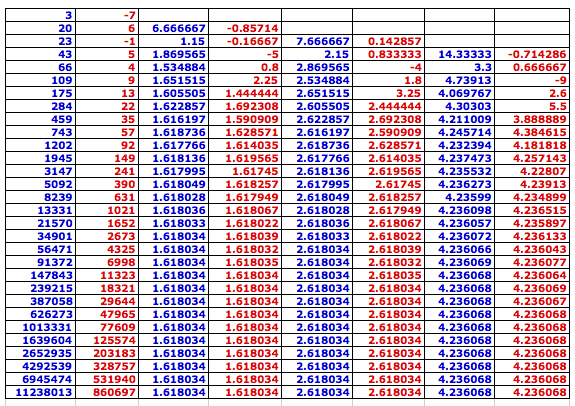
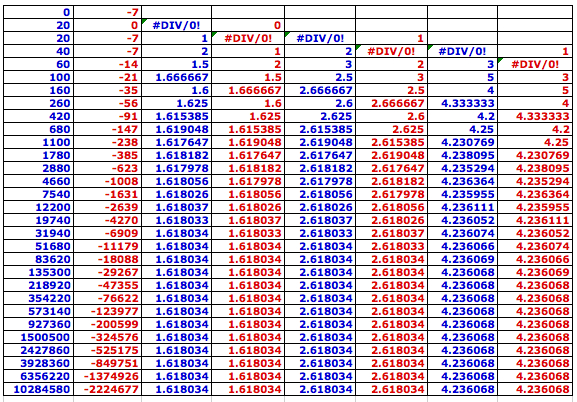
(2) Any integers a and b, a = b (not 0 simultaneously) or a > b:
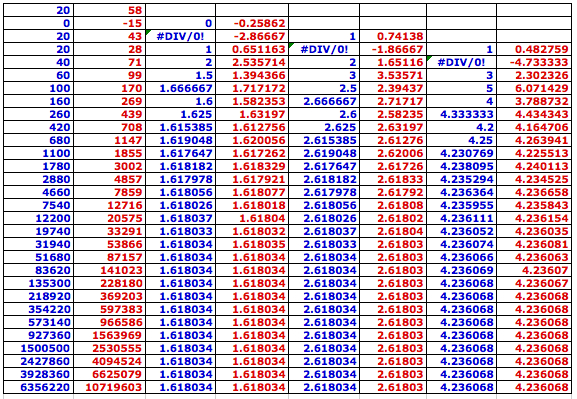
(3) Any real numbers a and b (not 0 simultaneously)
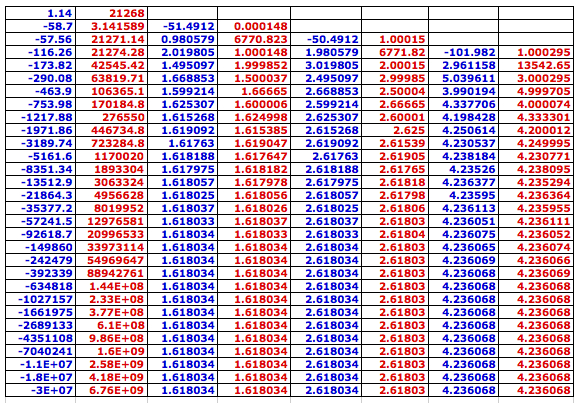
In conclusion, the initial conditions of the Fibonacci sequence does not affect the limit of the sequence of the ratio of successive terms of the Fibonacci sequence.