Exponential Functions

By

Hee Jung Kim

Let’s start with a number e. Mathematician Euler used the letter e for the first time, so it is sometimes called Euler’s number.

The number e is defined by the following equation:

for any positive integer n. If we put m = 1/n, then e is also defined by the equation:

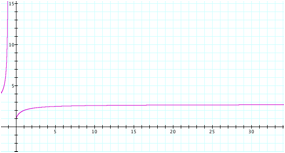
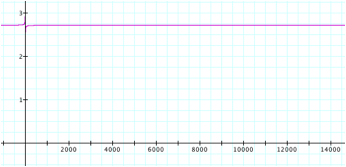
When we look at the graph of the function

and the behavior of the graph as x tends to the infinity, we can find that y approaches a value between 2 and 3. In fact, e is an irrational number and its value is 2.7182818284…

The number e is also the sum of the infinite series

where n! is the factorial of n. With Graphing Calculator 3.5 we can play with the upper bound of the summation, for example:

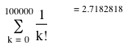
As the upper bound gets bigger and bigger, the sum approaches the number e.

Now we will observe the effects of nonzero real numbers a and b, and any real number c on the properties of the graph of the exponential function y based on e:

y = ae^bx + c

First, by setting c = 0, a = 1, let’s observe the effects of nonzero parameter b on the graphs of the exponential function:

y= e^bx

When b > 0, let’s explore the graphs.

If b > 1 and increases, the graph is shrunk horizontally.

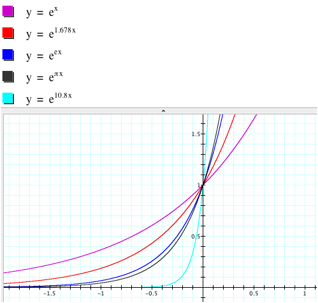
On the other hand, if 0 < b < 1 and decreases, the graph is stretched horizontally.

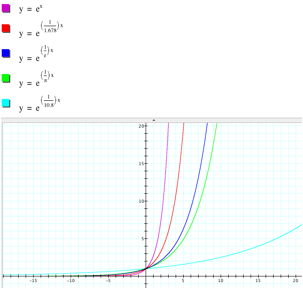
If b > 0, the graph of the exponential function is increasing viewed left-to-right. The graph is getting closer to 0 without touching the x-axis, so the x- axis is a horizontal asymptote to the graph.

How is the graph of the exponential function when b < 0?

If b < -1 and decreases, the graph is shrunk horizontally.

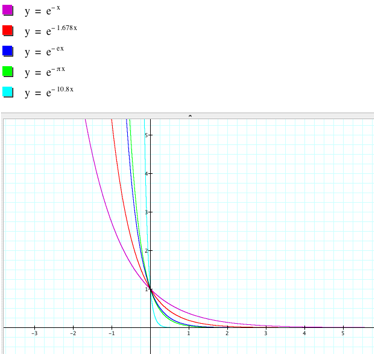
If -1 < b < 0 and increases, the graph is stretched horizontally.

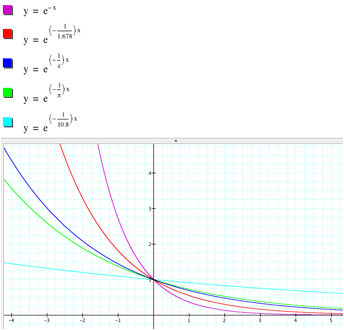
In sum up, when |b| > 1, the graph of y = e^bx is a horizontal shrink of the graph of y = e^x, and if 0 <|b|< 1, the graph of y = e^bx is a horizontal stretch of the graph of y = e^x.

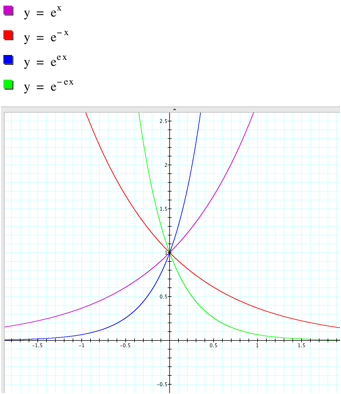
From the graphs, we find that for any nonzero real number b the domain of the exponential function y = e^bx is the set of all real numbers, and the range is the set of all positive real numbers because the graph is above the x-axis. The graph always passes through the point (0, 1). In addition, y = e ^{- bx} is symmetric with y = e^bx with respect to the y-axis, so is a vertical reflection of y = e^bx.

Now let’s observe the graph of the exponential function y = ae^bx when we multiply the function y = e^bx by a nonzero real number a. How does a affect the graph?

For simplicity, we consider y= ae^x by setting b = 1. If a > 1 and increases, the graph is stretched vertically.

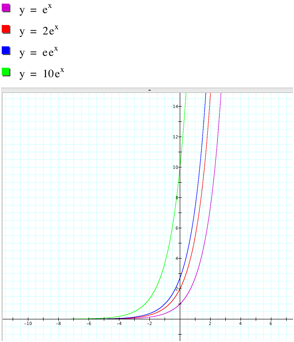
If 0 < a < 1 and decreases, the graph is shrunk vertically.

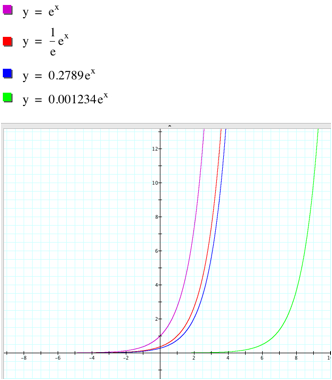
If a < -1 and decreases, the graph is shrunk vertically.

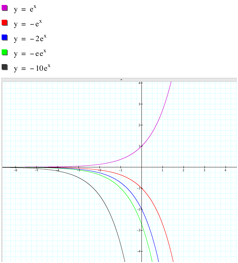
If -1 < a < 0 and increases, the graph is shrunk vertically.

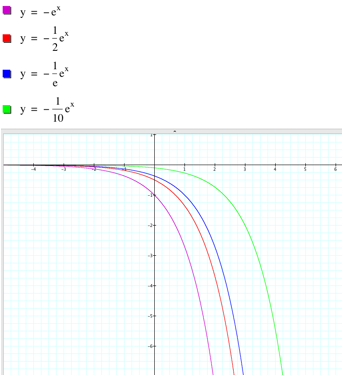
Therefore when |a| > 1, the graph of y = ae^bx is a vertical stretch of y = e^bx, and if 0 <|a|< 1, the graph of y = ae^bx is of a vertical shrink of y = e^bx. The graph always passes through the point (0, a). In addition, y = - ae^bx is symmetric with y = ae^bx with respect to the x-axis, so is a horizontal reflection of y = ae^bx.

Lastly, let’s observe the effects of parameter c on the graph of the exponential function y = ae^bx + c. For simplicity, let’s set a = 1, and b = 1. When c > 0 and increases, the graph of y = e^x + c is shifted up along the y-axis., and when c < 0 and decreases, the graph of y = e^x + c is shifted down along the y-axis.

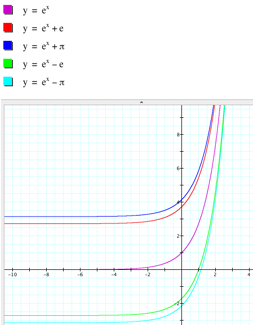
In general, c in the graph of y = ae^bx + c shifts the graph y = ae^bx in y-direction upward (c > 0) or downward (c < 0). Therefore the horizontal asymptote y = c is also shifted from y = 0 and the y-intercept is (0, 1 + c).

In this assignment we observed the effects of nonzero parameters a, b, and c on the graph of the exponential function y = ae^bx + c. a is related to dilation (stretch or shrink) in the y-direction, b is related to dilation (stretch or shrink) in the x-direction, and c is related to translation (upward or downward) in the y-direction.