by
Hee Jung Kim
We will use y instead of using b for this investigation.
I. We will consider the equation ![]() ,
and graph this relation in the xy plane.
,
and graph this relation in the xy plane.
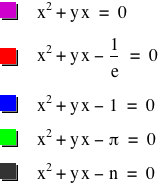
The graph of ![]() shows a straight line passing through the origin and the y-axis, and the graph of
shows a straight line passing through the origin and the y-axis, and the graph of ![]() is a hyperbola with two asymtotes x = 0 and y = - x , which can be represented by
is a hyperbola with two asymtotes x = 0 and y = - x , which can be represented by ![]() .
.
When n > 0, we get
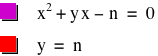
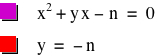
and
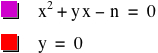
Therefore, the graph of ![]() always
intersects the horizontal line
always
intersects the horizontal line ![]() for
any real number b at two points whose x-coordinates are negative and positive
respectively. This implies that
for
any real number b at two points whose x-coordinates are negative and positive
respectively. This implies that ![]() for any real number b, n > 0 and n = 0 has always two real roots. In particular,
one of two roots is positive, and the other is negative.This is a nice approach
to investigate a pattern of roots of the quadratic equation
for any real number b, n > 0 and n = 0 has always two real roots. In particular,
one of two roots is positive, and the other is negative.This is a nice approach
to investigate a pattern of roots of the quadratic equation ![]() .
.
II. How about a pattern
of roots of ![]() for
n < 0? Again, by replacing b by y, we will consider the equation
for
n < 0? Again, by replacing b by y, we will consider the equation ![]() for
n < 0, equivalently
for
n < 0, equivalently ![]() for
n > 0, and its graph in the xy-palne.
for
n > 0, and its graph in the xy-palne.
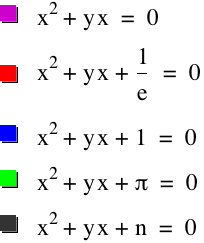
We note that even though ![]() and
and ![]() ,
n > 0 have the same asymptotes x = 0 and y =
- x or
,
n > 0 have the same asymptotes x = 0 and y =
- x or ![]() ,
their graphs are different hyperbolas. In this case, setting a constant
for n, say n = 1, let's vary y from -5 to 5. Then we have the following
animation.
,
their graphs are different hyperbolas. In this case, setting a constant
for n, say n = 1, let's vary y from -5 to 5. Then we have the following
animation.
The graph of a system of two equations can
be interpreted in relation of the solution pattern of ![]() for
different b as follows.
for
different b as follows.
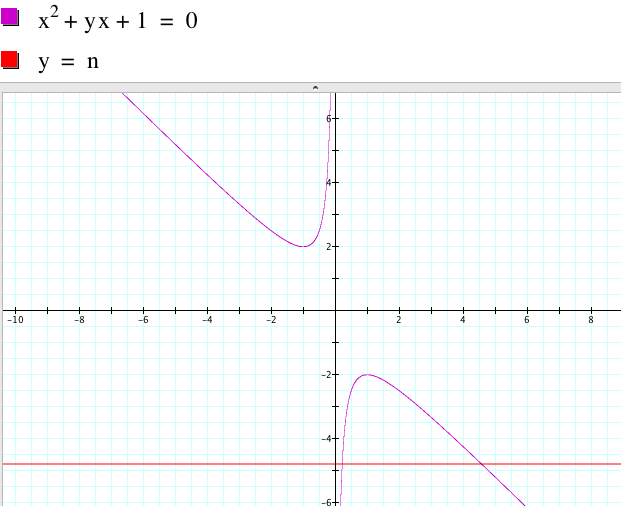
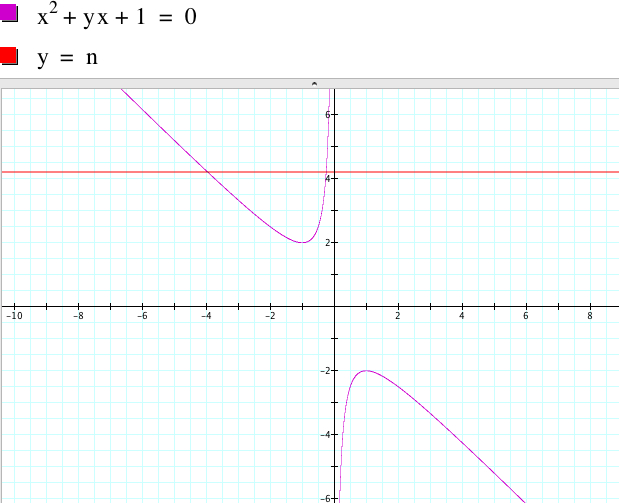
Case 1. ![]() has
two negative real roots if b > 2 because there are two points
of intersection
whose x-values are negative.
has
two negative real roots if b > 2 because there are two points
of intersection
whose x-values are negative.
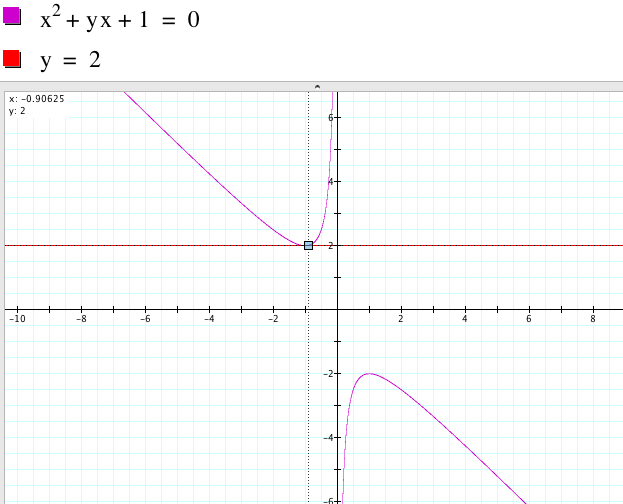
Case 2. ![]() has
one (repeated) negative real root if b = 2 because there is only one point
of intersection whose x-value is negative. The graph approximately shows
the root x = -1.
has
one (repeated) negative real root if b = 2 because there is only one point
of intersection whose x-value is negative. The graph approximately shows
the root x = -1.
Case 3. ![]() has
no real roots (in other words, two complex roots) for -2 < b <
2 because two graphs do not meet.
has
no real roots (in other words, two complex roots) for -2 < b <
2 because two graphs do not meet.
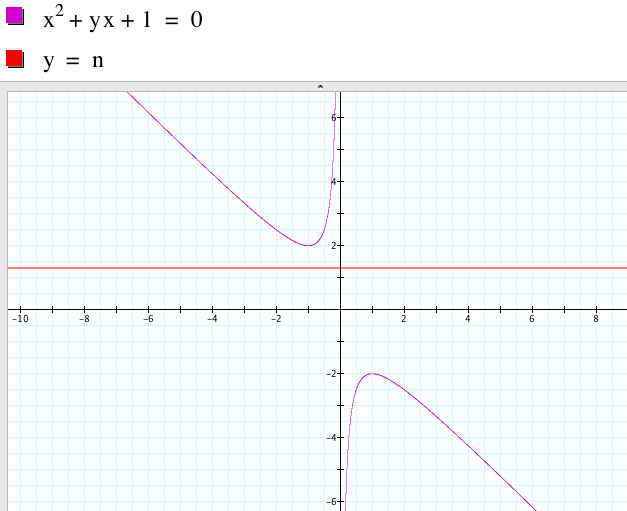
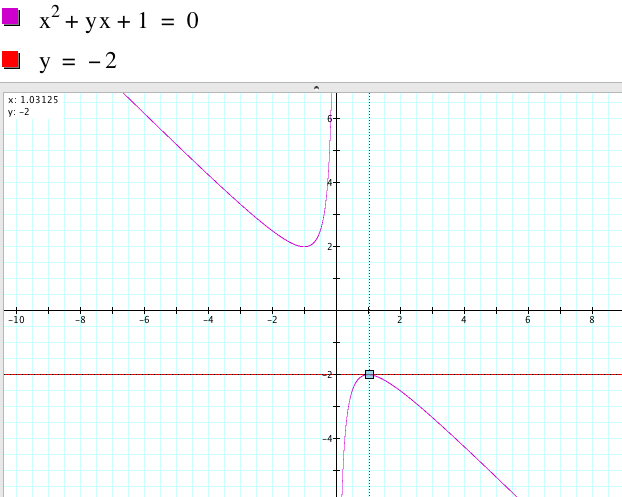
Case 4. ![]() has
one positive root if b = -2 because there is only one point
of intersection
whose x-value is negative. The graph approximately shows the root
x = 1.
has
one positive root if b = -2 because there is only one point
of intersection
whose x-value is negative. The graph approximately shows the root
x = 1.
Case 5. ![]() has
two positive real roots if b > 2 because there are two points
of intersection whose x-values are positive.
has
two positive real roots if b > 2 because there are two points
of intersection whose x-values are positive.