Centers of the medial triangle and the orthic triangle

by

Hee Jung Kim

 

I. Take any triangle ABC. Construct a triangle PQR connecting the three midpoints of the sides. This is called the medial triangle.

1.1. The medial triangle PQR is similar to the original triangle ABC.

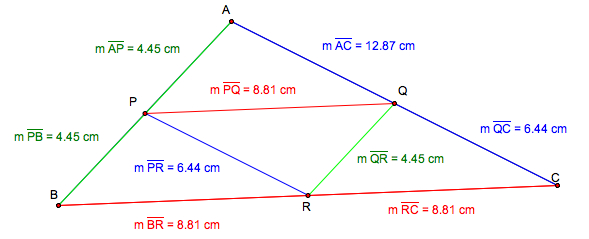
Proof. Since PQ, QR and PR are medsegments of BC, AB, and AC respectively, PQ =(1/2)BC, QR =(1/2)AB, and PR = (1/2)AC. Since the corresponding sides are proportional, Triangle PQR is similar to ABC.

1.2. The area of the medial triangle PQR is one fourth of the original triangle ABC.

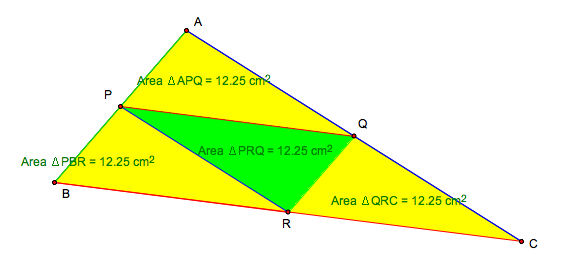
Proof. Since four triangles APQ, PBR, PQR, and RQC are all congruent (SSS), the area of ABC is four times of the area of one of those four triangles, say, PQR. Therefore, area of PQR = (1/4)area of ABC.

1.3. Let's construct G, H, C, and I for PQR and visually compare them with G, H, C, and I for ABC. (See GSP)

1.4. The centroid of the original triangle ABC = The centroid of the medial triangle PQR.

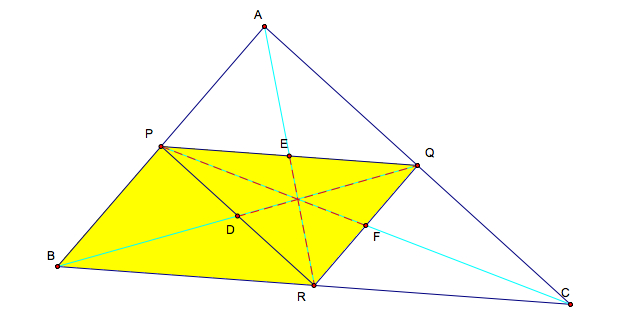
Proof. We must show that the medians of ABC pass through the midpoints of three sides of the medial triangle PQR. Since PQ is a midsegment of ABC, PQ//BC, so PQ//BR. And since QR is a midsegment of AB, AB//QR, so QR//PB. By definition, a quadrilateral PQRB is a parallelogram. The medians BQ and CP are in fact the diagonals of the parallelogram PQRB. The diagonals of a parallelogram bisect each other, so PD = DR. In other words, D is the midpoint of PR. In the similar manner, we can show that F and E are midpoints of RQ and PQ respectively.

1.5. The loci of four centers of the original triangle ABC and the median triangle PQR respectively can be found and compared while one vertex, say A, of ABC moves along a line segment or a circle of ABC. (See GSP)

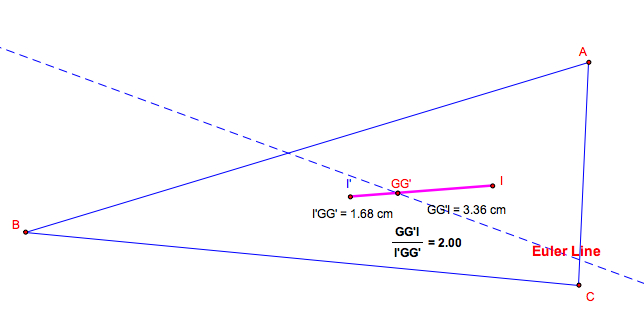
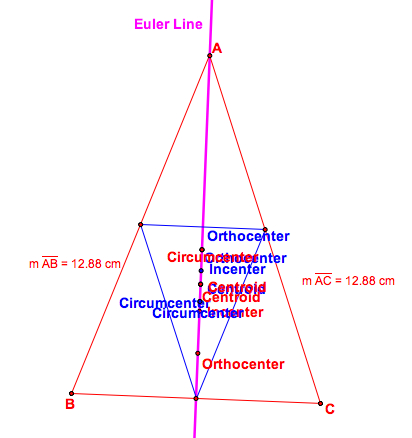
1.6. In general, the incenter is not on the Euler line. If we connect the incenter I of the original triangle ABC and the incenter I' of the median triangle PQR, the centroid G of ABC which coincides with the centroid G' of PQR divides the line segment I I' in a ratio of 2 to 1.

1.7. When the original triangle ABC is an isosceles triangle, the Euler line of ABC coincides with one of the median triangle PQR.

II. Take any triangle ABC. Construct a triangle connecting the feet of the altitudes. This is called the orthic triangle DEF. Construct G, H, C, and I for the orthic triangle.

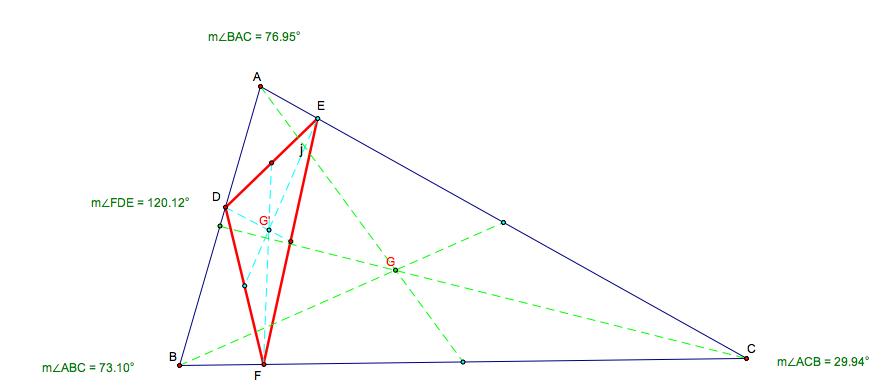
2.1. Compare the centroid G of the original triangle ABC and G' of the orthic triangle DEF.

(a) If ABC is an acute triangle, DEF is an obtuse triangle. G and G' do neither coincide nor have any relationship.

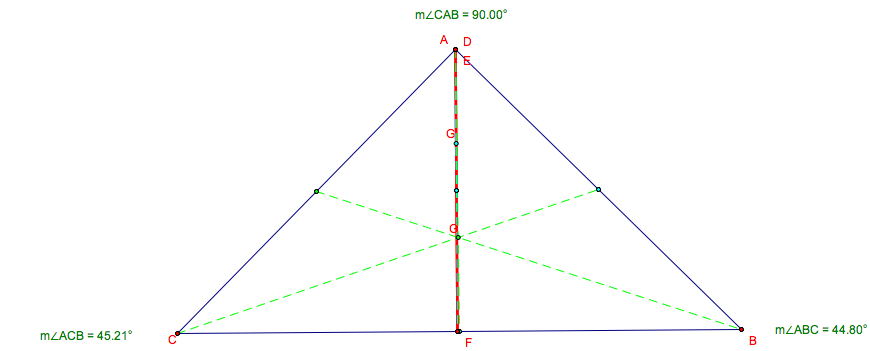
(b) If ABC is a right triangle, DEF will be degenerate.

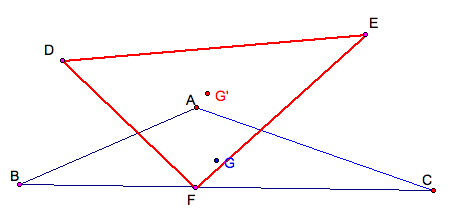
(c) If ABC is an obtuse triangle, DEF is an acute triangle. G and G' do neither coincide nor have any relationship.

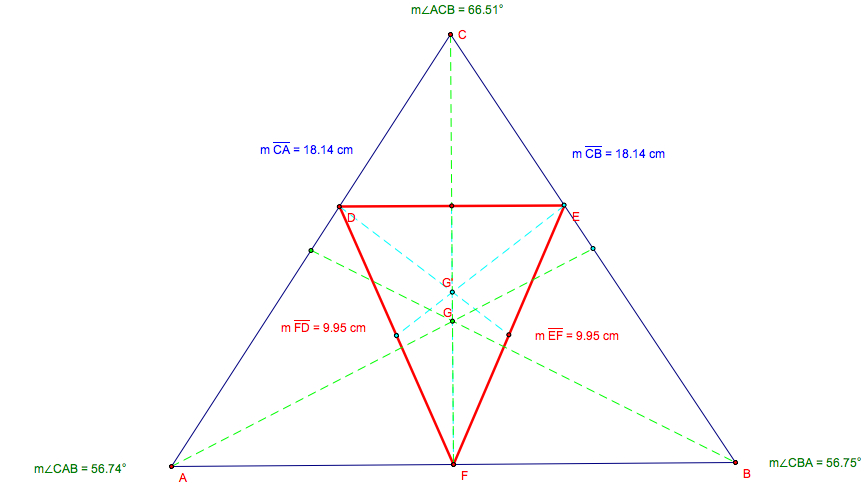
(d) If ABC is an isosceles triangle, then so is DEF, and G and G' are on the same line.

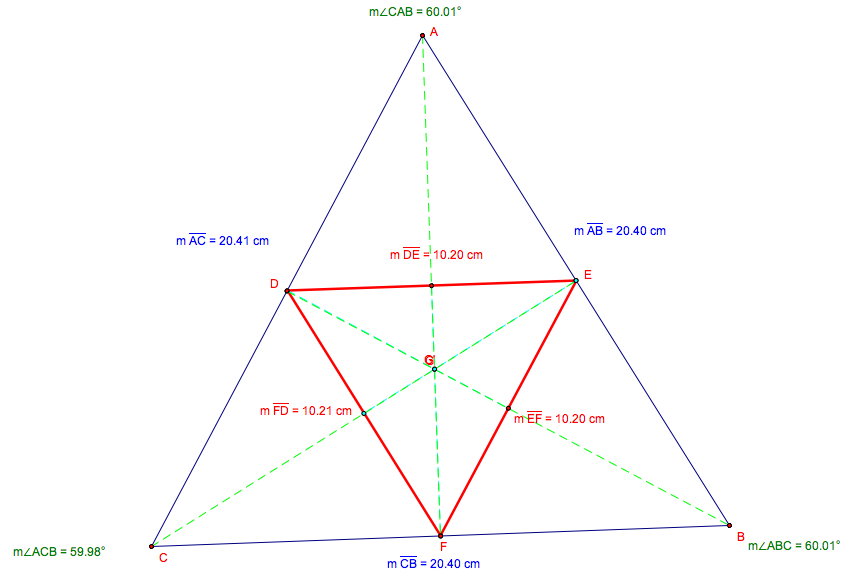
(e) If ABC is a equilateral triangle, so does DEF, and G and G' coincide because DEF is the medial triangle.

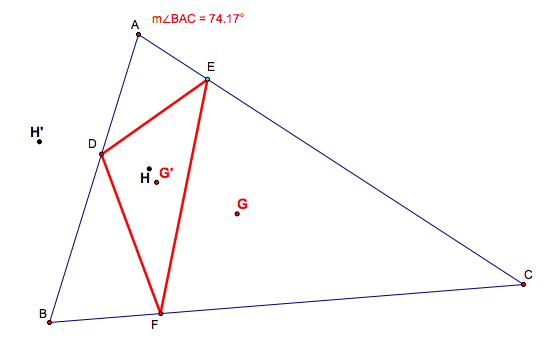
2.2. Compare the orthocenter H of the original triangle ABC and H' of the orthic triangle DEF.

(a) When ABC is an acute triangle, since DEF is an obtuse triangle, H' is outside of DEF. H and H' do neither coincide nor have any relationship.

2.3. Compare the circumcenter C of the original triangle ABC and C' of the orthic triangle DEF.

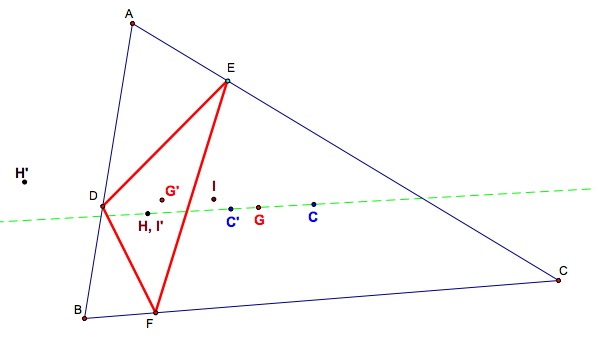
(a) H, C, C', G are on the same line.

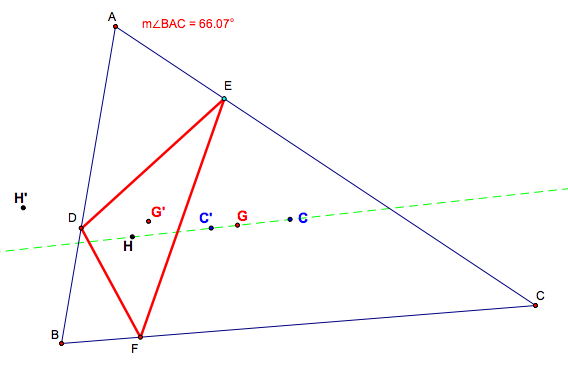
2.4. Compare the incenter I of the original acute triangle ABC and I' of the orthic triangle DEF.

(a) The angle bisectors of DEF pass through one of the vertices of ABC.

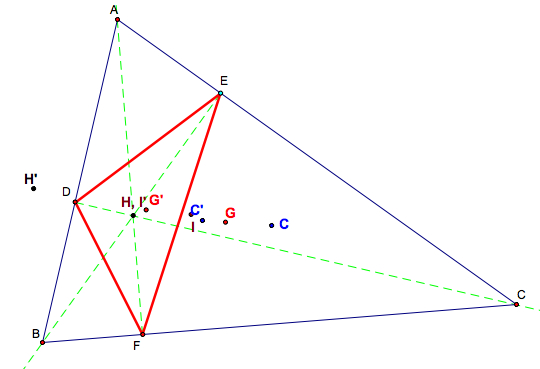
(b) H and I' coincide (for acute triangles), so H, I', C, C', G are on the same line.

2.5. Let a vertex, say A, of ABC be moving along a line segment. The we have the following loci of all four centers of ABC (blue) and PQR (red) (See GSP):

The locus of the centroid G of the original triangle ABC is a line segment parallel to the given segment, and the locus of G' of PQR is a curve.

The locus of the orthocenter H of the original triangle ABC is a curve, and the locus of H' of PQR is a parabola passing through the vertices B and C of the base BC.

The locus of the incenter I of the original triangle ABC is a curve, and the locus of I' of PQR is part of a parabola passing between B and C which overlaps with the locus of the orthocenter H of ABC because H and I' coincide only for acute triangles.

The locus of the circumcenter C of the original triangle ABC is a line intersecting the given line, and the locus of C' of PQR is a curve.

2.6. Let a vertex, say A, of ABC be moving along a circle when the base BC of the triangle ABC is a chord of the circle. In fact, the circle is the circumcircle of ABC. The we have the following loci of all four centers of ABC (blue) and PQR (red) (See GSP):

The locus of the centroid G of the original triangle ABC is a circle, and the locus of G' of PQR is an ellipse.

The locus of the orthocenter H of the original triangle ABC is a circle passing through the vertices B and C, and the locus of H' of PQR is a curve.

The locus of the incenter I of the original triangle ABC is a closed curve, and the locus of I' of PQR is a part of circle passing through B and C.

The locus of the circumcenter C of the original triangle ABC is fixed, and the locus of C' of PQR is a curve.