Investigation on

by

Ana Kuzle

For this problem I begin by graphing several examples of a given problem for p=2,3,4, and 5.

Here are their corresponding graphs.

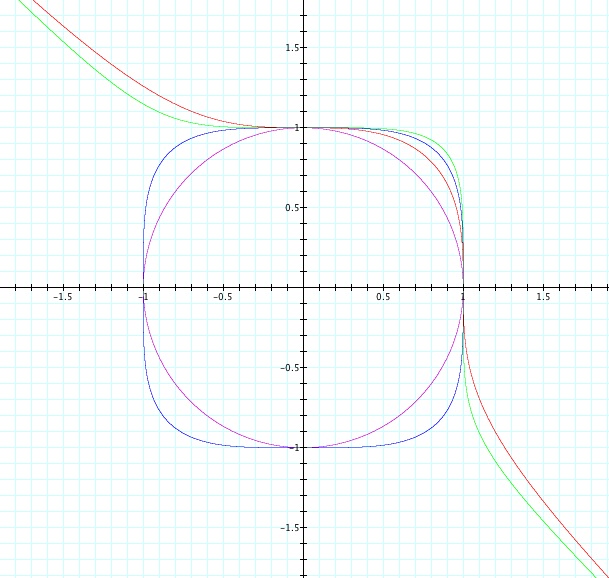
For, p=2 I knew that I would get a circle with center at the origin and radius 1. For p=3 I got a curvature, for p=4 I got a shape looking as a curved square. In the end of this first exploration for p=5 I got a curve.

From the graphs we can also observe that for chosen p the points (1,0) and (0,1) lie on this graphs.

From the picture we can also observe that the graphs of even powers of the equation and odd powers of the equation converges to each other between -1 and 1. 

So, given different exponents (even, odd) we get two possibilities.

I. First we investigate the set

.

Changing parameter p we get different p-circles. As p grows to infinity circle transforms into a square.

Thus, for even exponents we get a compact, or more precisely a closed contour.

II. Let us now investigate the set

.

Again, by changing the parameter p we get different graphs.

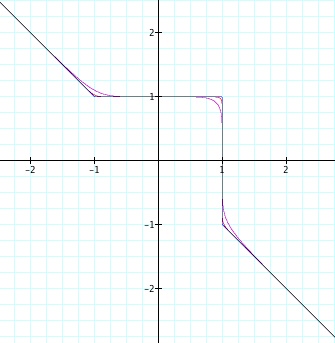
By increasing parameter p each curve will be above the previous curve between 0 and 1, but below the curve for the other values of  x.

Thus, for odd p we get a graph of a function where p-root is defined for any real number. As p goes to infinity the curve becomes a 'broken line'.

III. An idea to look at the same equations with negative exponents came naturally.

From the picture we can see that graphs with negative even exponents look alike, as well as those with negative odd exponents which also have a common point and that is the origin of coordinate system.

Combining all of the above gave me this.

And combining following ones gave me this:

As I wanted to get functions symmetrical in respect with the origin I combined functions mentioned above with the same functions but with -1 in the end instead of 1. Combining those functions gave me this.