

Centers of a Triangle
by
Ana Kuzle
I decided to explore the relationship between some characteristic points of a triangle. First, I will introduce the labels I have used.
G denotes the CENTROID of a triangle, that is the common intersection of the three medians of the triangle. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
H denotes the ORTHOCENTER of a triangle, that is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
C denotes the CIRCUMCENTER of a triangle, that is the point in the plane equidistant from the three vertices of the triangle.
I denotes the INCENTER of a triangle, that is the point on the interior of the triangle that is equidistant from the three sides.
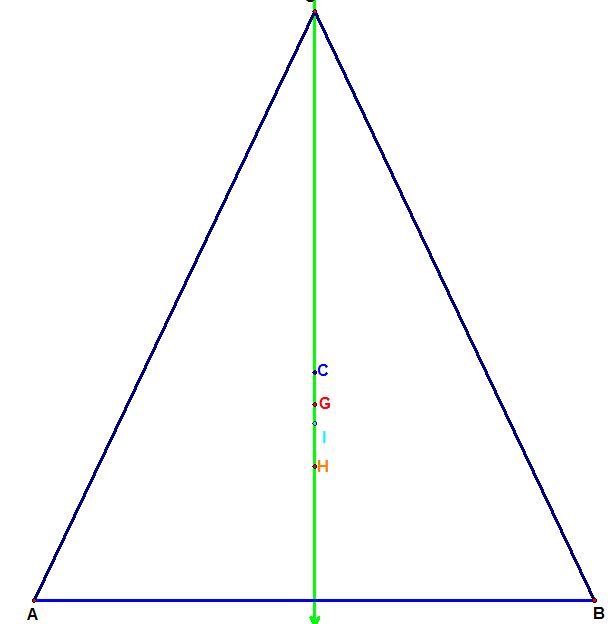
I. First, I tried to find some relationship between those four points. After trial and error method I was able to discover that G, H and C are collinear as shown below as well.

Q.E.D.
II. Then, I was interested in which relationship are all four of the point given. I measured all the lengths and I continued exploring by moving one of the triangle points. As the sides AC and BC were getting equal point I was becoming closer to the line. When my scalene triangle became isosceles all for points were collinear.
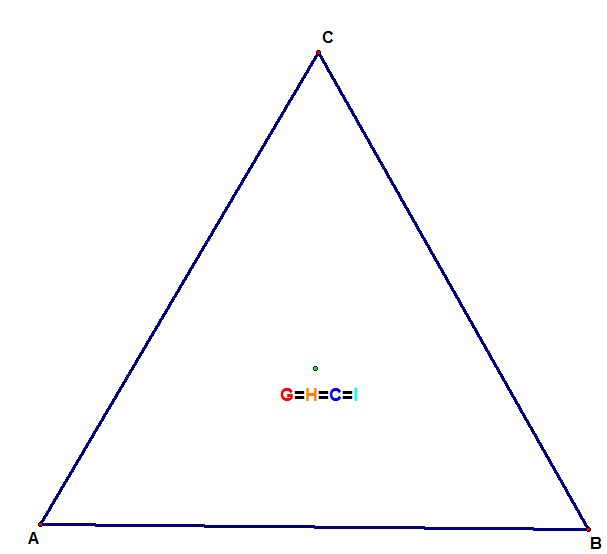
III. In the end I decided to see what the connection was if the triangle was equilateral. As you can see below, there was no line. All four points coincide.
Thus, G=H=C=I.
IV. Since, relationships were determined by the type of a triangle I decided to explore whether there are more connections between those points regarding their lengths. I measured all the lengths and saw that ![]() .
.
V. It was interesting to see how type of a triangle affects position of triangle centers concerning the triangle.
I and G remain inside the triangle regardless of triangle type. That was not the case for C and H. In an acute triangle there were as well inside the triangle but in an obtuse triangle H and C were outside the triangle.
Secondly, in a right triangle C lies on the midpoint of hypotenuse and H meets with a vertex at the right angle.
Note: All of the investigation is in one file containing three sketches. It is here. Furthermore, the line investigated above is called Euler's line.
VI. After some time I discovered this or look bellow.
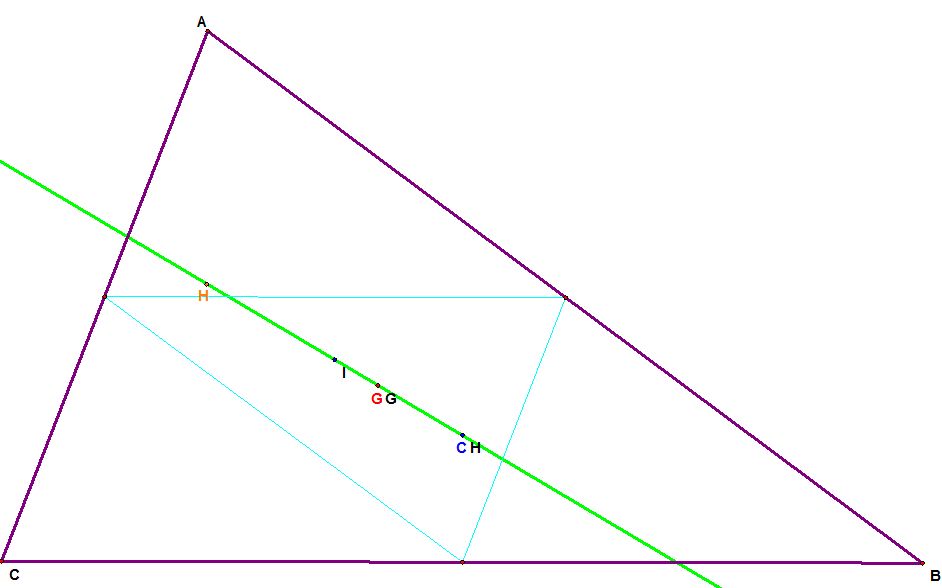
What can we see from the picture where the blue triangle is a mid triangle of the original one.
1. Euler's line of the mid triangle is the Euler's line of the original triangle
2. Centroid of both triangles are the same
3. Orhocenter of the mid triangle is the circumcenter of the original triangle
Conclusion: The Euler line is its own complement.
VII. It occurred to me that I can explore the loci of these centers as a vertex of the triangle is animated along a segment. To my surprise I got a pretty neat result, especially for the locus of the orthocenter.
I constructed the locus of the orthocenter as a vertex of the triangle is animated along a segment.
In detail:
1.Draw a segment across the top vertex.
2. Merge point to segment in edit menu.
3. Animate vertex on that line segment.
4. Trace Orhocenter.
5. Start animation.
The result is shown below.
From the picture shown we can conjecture that the generated curve is a parabola.
VIII. See what happens when G, H and C are traced. Thus, loci of those triangle centers.
IX. Natural thing was to do this as well. See the animation here.
X. I will finish my investigation with showing the locus of Euler segment (segment connecting H and C).
The picture below does not give a full insight. So, change the free line segment or the triangle and see the changes. For that click here.
XI. Tracing the locus of the incenter I got this! I was amazed.
Bellow there are two situations. Click here to get more.