Problem: Find a construction for a point P such that the sum of the distances from P to each of the three vertices is a minimum
by
Ana Kuzle
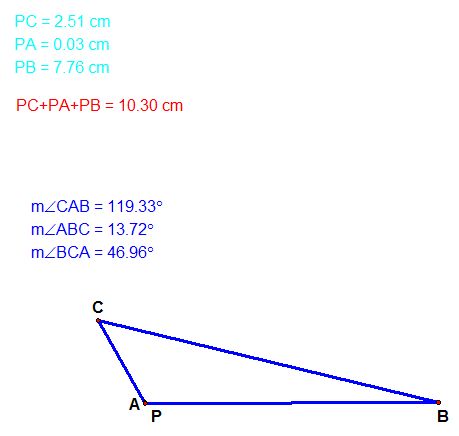
I. Before I could construct such a point I had to find it. I began therefore by exploring this problem by moving the point P. As I was moving point P closer to the sides the sum was getting bigger therefore I was moving it inside the triangle. At some point I stumbled upon the smallest I could discover. You can move the point as well (or let GSP do it for you).
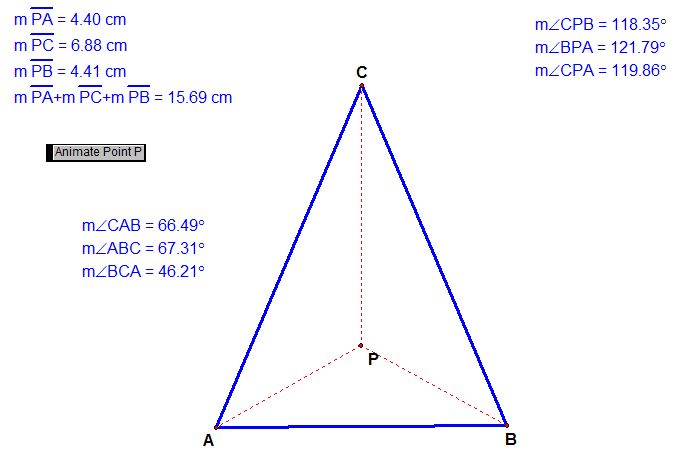
As you can see I measured the angles as well. This gave me an idea. Or more precisely, I had a conjecture: Point P such that the sum of the distances from P to each of the three vertices is a minimum when ![]() .
.
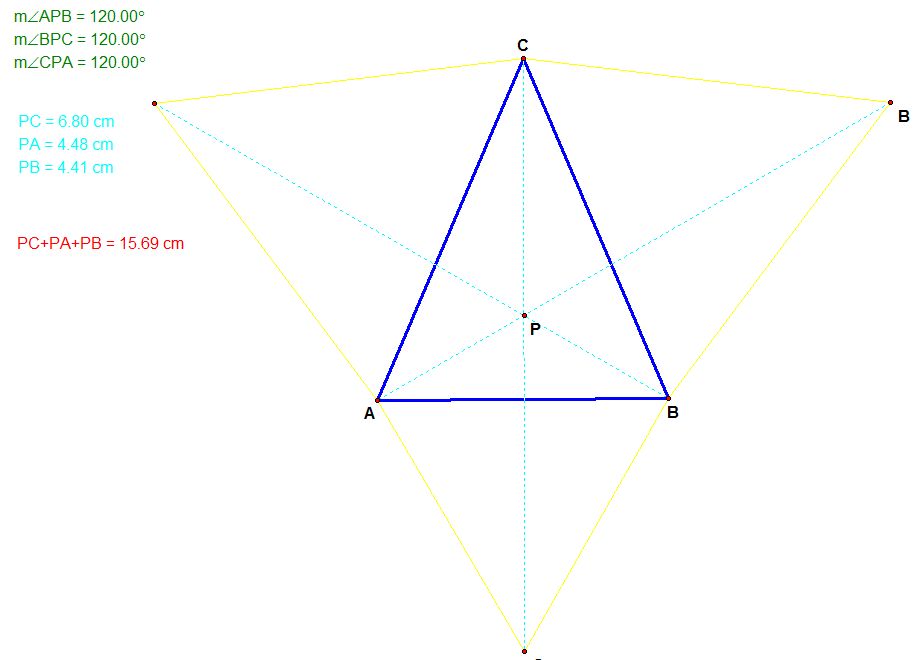
II. Construction of point P is shown bellow.
Steps:
1. construct equilateral triangles on each of the sides
2. connect opposite vertices
3. point P is the intersections of segments in 2.
You can find this steps done in GSP.
III. Proof.
We know that if the triangle ABC has an angle whose measure is greater or even than 120°, then the point P is outside the triangle or of the vertices of the triangle ABC, respectively. Also, from the construction we have seen that if the measure of all angle is less than 120°, than the point P lies inside the triangle ABC.
Suppose that measure of each angle ABC is less than 120°. Let's start by extending CP through P, and BP through P. Also, by drawing perpendiculars from A to just obtained segments we get points D and E respectively. In this way we got two right-angled triangles. But moreover we get that PD=1/2 AP, and PE=1/2 AP since <APE=<APD=60°, and <PAE=<PAD=30°. Furthermore, CD<AC, and EB<AB since the hypotenuse is always longer than the legs of the triangle. But, CD=CP+PD=CP+1/2 AP. And, EB=EP+PB=PB+1/2 AP. Thus, AP+BP+CP=1/2 AP+1/2 AP+BP+CP=CD+EB<AC+AB. Hence, the point P is better than vertex A. With no loss of generality, P is better than B, and C for the same reasons. Therefore, having all angles of measure less than 120° point P gives the minimal sum.
|
IV. I discovered as well that if angles of a triangle are less than 120 then point P is inside the triangle, meanwhile when one of the angles is greater than 120 then point P is outside the triangle.
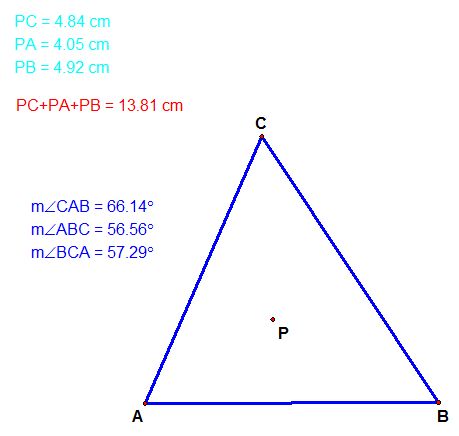
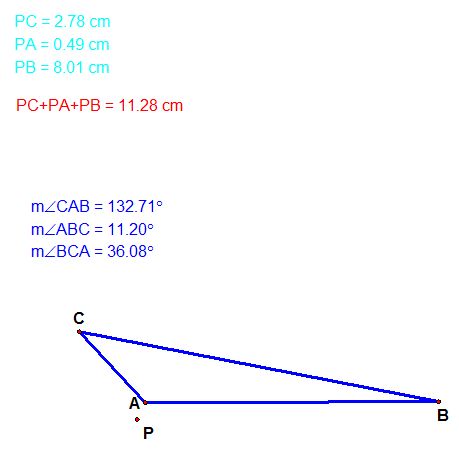
It is obvious that point P is not the minimum then since it is outside the triangle. Where is the minimum then? Well, it is in the vertex whose angle is greater than 120.