---

Tangent circles

by

Ana Kuzle

The purpose of this assignment is to investigate tangent circles. Thus, given two circles and a point on one of the circles find a circle that is tangent to both circles with one point of tangency being the designated point.

I. There are several cases to take under consideration.

I begin with with two circles, one inside of the other, and a given point of tangency on the large circle. Using the following construction tangent circle was found. Also, script tool for it is here.

In the picture bellow, the red circle is our tangent circle.

If we animate the point of tangency on the bigger circle and measure in the same time we can see that the sum of the segments from the center of the given circles to the center of the tangent circle is constant. Thus, the locus of the tangent circle in an ellipse with focal points in the centers of given triangles.

An ellipse is defined as the set of all points in the plane whose sum of distances from two fixed points (focal points) is constant. Given that, we can construct an ellipse as follows.

If we trace the center of the tangent circle we get an ellipse.

Even better, if we trace the perpendicular bisector of the base on an isosceles triangle we get a bundle of tangents that describe an ellipse. Animation is given here.

II. Second case that I have observed was when the circles intersect each other. Again I used the same construction. In the picture bellow, the red circle is our tangent circle.

If we animate the point of tangency on the bigger circle and measure in the same time we can see that the sum of the segments from the center of the given circles to the center of the tangent circle is constant. Thus, the locus of the tangent circle in an ellipse with focal points in the centers of given triangles.

Even better, if we trace the perpendicular bisector of the base on an isosceles triangle we get a bundle of tangents that describe an ellipse. Click here for animation.

III. I continued by looking at the tangent circle of two circles which are tangential to each other. In the picture bellow, the red circle is our tangent circle.

In this case the loci are two parabolas where the distance of the given circles and the tangent circle is constant. The picture bellow shows the construction of the parabolas when the loci and perpendicular bisector of the isosceles triangle is traced. Click here for the animation.

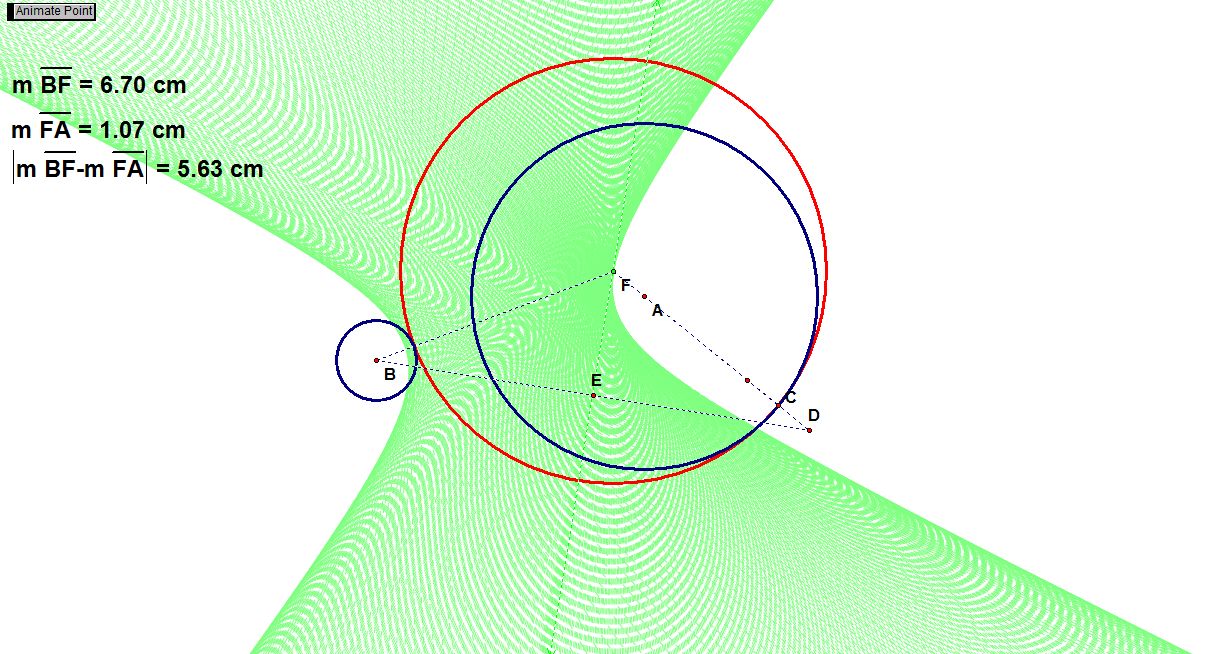
IV. In the end I looked at the case when two circles were disjoint. If we animate the point of tangency on the bigger circle and measure in the same time we can see that the absolute value of difference of the segments from the center of the given circles to the center of the tangent circle is constant. Thus, the locus of the tangent circle in a hyperbola with focal points in the centers of given triangles.

A hyperbola is defined as the set of all points in the plane whose absolute value of distances from two fixed points (focal points) is constant. Given that, we can construct a hyperbola as follows.

If we trace the center of the tangent circle we get a hyperbola.

if we trace the perpendicular bisector of the base on an isosceles triangle we get a bundle of tangents that describe a hyperbola. Animation is given here.