Quadrilaterals Revealed
by
Ana Kuzle
Polygon is defined as a closed plane figure with n sides. The origin of the word comes from greek poly meaning many and gonia meaning angle. The can be classified in several ways. Based on the length of the sides the polygon is regular or irregular if the sides are congruent or not congruent respectively. Polygons can also be classified as convex, concave or star polygons. In order to classify polygon as being convex or concave we can look at the more general situation. In Euclidean space, an object is said to be convex if for every pair of two points within the object, a straight line segment that joins them is also within the object.
A planar polygon is convex if it contains all the line segments connecting any pair of its points. A planar polygon that is not convex is said to be a concave polygon. A star polygon is a non-convex polygon which looks in some way like a star. A star polygon is a self-intersecting polygon, created by connecting one vertex of a simple, n-sided polygon to another, non-adjacent vertex and continuing the process until the original vertex is reached again.
A polygon with 4 sides is called a quadrilateral or a tetragon or a quadrangle. Two sides are said to be adjacent or opposite based whether they have or do not have a vertex in common. Analogously, two vertices are said to be adjacent or opposite according as they do or do not belong to one side. A line containing two opposite vertices are called diagonals. Similarly, there are three topological types of quadrilaterals: convex quadrilaterals, concave quadrilaterals, and crossed quadrilaterals (or butterflies, or bow-ties).
Looking at the figure above we can notice that for a convex quadrilateral, both diagonals are inside; for a concave quadrilateral, one is inside whilst the other one outside; and for a crossed quadrilateral both of the diagonals are outside the quadrilateral.
We can define the area for each of the quadrilateral types. Observing first the convex quadrilaterals we can see that the area of a convex quadrilateral can be expressed as the sum of the two areas divided by any of the diagonals,
A(ABCD)=A(ABC)+A(CDA)=A(BCD)+A(DAB). Since, we introduced topologically different quadrilaterals we are going to introduce area being positive or negative based on the fact whether the vertices are named counterclockwise or clockwise. For instance, A(ABC)=A(BCA)=A(CAB)=-A(CBA).
Thus, the area of a concave quadrilateral can be expressed by A(ABCD)=-A(ACD)+A(ABC)=A(ADC)+A(ABC).
Similarly, the area for the crossed quadrilateral equal A(ABCD)=A(ACS)-A(SDB).
A special type of quadrilaterals are cyclic and tangential quadrilaterals. Both of these two types have interesting properties and we will explore some of these.
Cyclic quadrilaterals
A cyclic quadrilateral is the class of quadrilaterals for which a circle can be circumscribed outside the quadrilateral such that its vertices all lie on a single circle.
Property 1.
Property 2.
Property 3.
Property 4.
If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P perpendicular to any side bisects the opposite side.
Ptolemy's Theorem.
The product of the lengths of the two diagonals of a cyclic quadrilateral as equal to the sum of the products of opposite sides.
An important theorem of the plane geometry is Heron's formula which is credited to the famous Greek mathematician Heron of Alexandria (10–70 AD). Given the length of the sides a, b and c, and perimeter s of the triangle, Heron's formula gives the area of the triangle ABC as function of its sides,
Question: Does the analogue of the Heron's formula apply for quadrilaterals? What would this formula look like?
Conjecture:
Experiment:
Square |
Rhombus |
Rectangle |
For a square of side length a, we know that its area equals a^2. Perimeter of square is equal to s=(a+a+a+a)/2=2a. Hence,
|
For a rhombus of side length a, we know that its area equals
|
For a rectangle of side lengths a and b, we know its ares equals A=ab. Perimeter of the rectangle is equal to s=(a+a+b+b)/2=a+b. Hence,
|
Notice that the conjecture applies for squares and rectangles but not rhombuses. What do square and rectangle have in common, different form the rhombus properties?
Whilst square and rectangle are cyclic quadrilaterals, rhombus is not. Thus, we can conjecture that the analogue of the Heron's formula apply only for cyclic quadrilaterals.
The area of a cyclic quadrilateral is the function of the lengths of its sides. This theorem is a contribution by an Indian mathematician and astronomer Brahmagupta (598–668).
Property 5. The angle bisectors of the lines containing opposite sides of an inscribed quadrilateral meet at right angles.
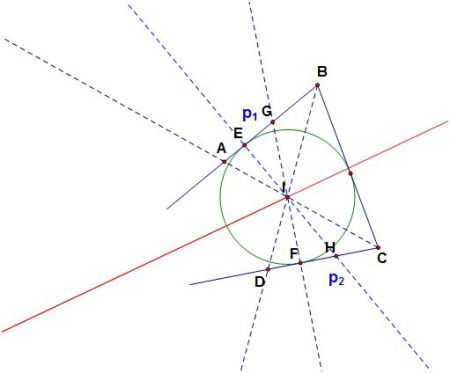
| The picture shows the elements given, as well as all of the conclusions. From the picture and the problem given we are trying to prove that <FGE=90º. But, we can restate this as wanting to prove that the ΔFEH is an isosceles triangle, or that ΔFGEΔHGE, since those two triangles share the same side GE, and angles <FEG=<GEH are congruent since line EG is the bisector of the <AEB. Notice that <EFG=m1+l2, and <EHG=l1+m3 because the interior angle is always the same as the sum of its corresponding exterior angles (1). Also, we know that l1=l2 because of the angle bisector, and that m2=m3 because the vertex angles are congruent. Therefore we get that l2+m1=l1+m3. From this we get that <EFG=<EHG using again (1). Using AAS theorem we now know that the triangle ΔFEH is an isosceles triangle. But one of the properties of an isosceles triangle that the vertex bisector is the altitude of the triangle. Hence, we can conclude now that <FGE=90º. Therefore we have proven that the angle bisectors of the opposite sides of an inscribed quadrilateral meet at right angles. |
Imagine a sheet of paper with two line segments drawn on it, as shown. Without extending the paper or the lines segments, construct the bisector of the angle determined by two line segments.
| One of the strategies would be to use conclusions from problem above (Property 4.) since we have proven that. Given two line segments, we need to construct an arbitrary circle that intersects those two lines. By doing that we get a cyclic quadrilateral ABCD whereas AB and CD are given two line segments (p1 and p2 lines). Extending segments AD and BC and we can extend those two, we get the point E. Hence, we can construct the angle bisector y of the angle < AEB. We have one line that contains the angle bisector, and from the problem before we know that the other angle bisector l will be perpendicular to y. But we know we cannot construct it just anywhere, so the question is where. But, if we look at the picture above from the Angle Bisectors Problem, we can construct a parallel line to the angle bisector y through vertex C. Notice that obtained line segment CX is going to be perpendicular to the angle bisector l. Furthermore, if we look at the constructing done in the previous problem we can conclude that the triangle Δ CIX is an isosceles triangle since the line l is the bisector. Hence, by constructing a midpoint Z on the segment CX we get a point on that bisector. Knowing that the bisectors intersect and a right angle, the line obtained by constructing a perpendicular line to y through Z we get the angle bisector of the originally given lines p1 and p2. |
| Constructing parallel lines to given ones. The new parallel lines would have to be close enough to intersect. Afterwards, constructing its bisector is trivial. And it is the solution of the original problem since the lines were parallel so the measure of the angle is preserved. | 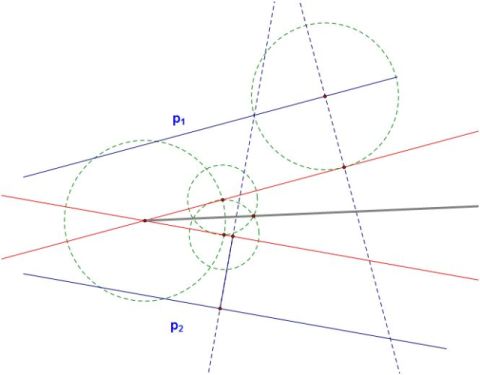 |
In order to construct a circle tangent to both lines, I connected the endpoint getting segment BC. Hence, I wanted to construct an incircle to the ``broken’’ triangle because an incircle is tangent to the segments of a triangle. Notice that incircle is an inscriber circle such that the distance to the sides is the same and equal to the radius of the incircle. Hence, I constructed angle bisectors of angles <ABC and <BCD, and their intersection is the incenter I. To construct the incircle I constructed the perpendiculars to lines AB and CD because the distance from the incenter to those sides must be the same. Hence, the angle <GEI=<HFI=90º. |
 |
Tangential quadrilaterals
A tangential quadrilateral is the class of quadrilaterals for which a circle can be inscribed inside the quadrilateral so that each side of the quadrilateral is tangent to the circle.
Property 1.
Property 2.
Property 3.
Property 4.
Bicentric quadrilaterals
A quadrilateral is said to be bicentric if it is cyclic and tangential.
Notice that we have shown the Brahmagupta's Theorem that is valid for cyclic quadrilaterals, and that the property of the sum of the opposite sides being equal is valid for tangential quadrilaterals. Combining those two theorems we can deduce about the area of the bicentric quadrilaterals.
As expected the area of a bicentric quadrilateral is also function of the lengths of its sides.
Midpoint quadrilaterals
A midpoint quadrilateral is the quadrilateral formed by connecting the midpoints of the 4 sides of the original quadrilateral.
Question 1: What is the midpoint quadrilateral of an arbitrary quadrilateral ABCD?
Similar questions can be pursued such as:
But let look as some more interesting problems instead.
Trisection of a quadrilateral
Something Golden
The golden ration, also know as the golden section or the divine proportion is a number often encountered in mathematics, arts, architecture, nature, etc.
Two quantities are said to be in the golden ratio if the sum of those quantities and the larger one is the same as the ratio between the larger one and the smaller one. The constant is commonly denoted by Greek letter and approximately equal to 1.6180339887.
Golden Rectangle
Golden rectangle is a rectangle whose sides are in the golden ratio.
Golden Rectangle Construction
| Something cool: Successive points dividing a golden rectangle into squares lie on a logartihmic spiral. |
Some other interesting problems
Problem 1.
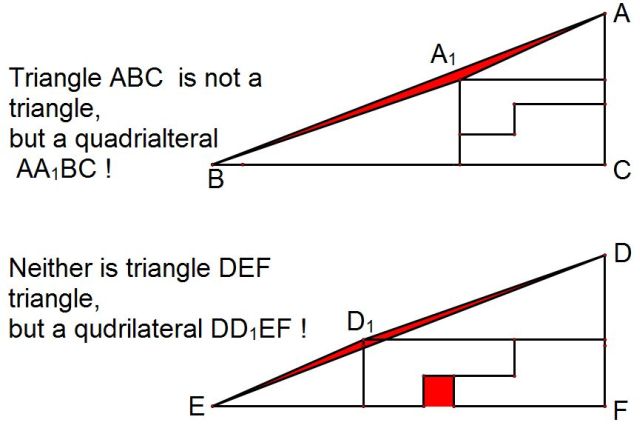
The picture bellow is a quadrilateral and not a triangle believe it or not. There are several ways of proving that statement. |
This is a problem from the 1953. It was apparently posed by a man by the name of Paul Curry who was an amateur magician from the New York. |
Picture on the right will be used in proving. |
Let us calculate the area of a big triangle in two ways assuming that the length of each side of a square greed represents one unit length. |
If the origin is a triangle, then the red and the blue triangle should be similar. However, |
Similarly we can look at the tangent of vertex A, and if the origin is a triangle they should be the same. However, if we look at the tangent of vertex A of a red triangle and the origin triangle, then |
Using analytical geometry we can use different concepts. For that we will use the following representation, |
If AB is a line than Plugging the numbers into (1) we get 5.385+8.544=13.92913.928 unit length. |
If AB is a line, then points A, A1 and B should be collinear. Hence, A (Δ AA1B) should be equal to zero. But,
|
If AB is a line, then A1 should lie on the line. However, equation of the line passing points A and B is
If we plug coordinates of point A, then we get |
Problem 2.
The 8x8 square is cut into four pieces. The pieces are fitted together in different way. But the square has area 64 and the rectangle 65. Explain the paradox.
Detail solution of this problem is not needed. Every strategy that was used in the example above can also be applied.
For instance, the area of a ``rectangle’’ can be calculate in two ways.
On one hand, A=13·5=65 square units, and on the other hand A=2·8·3/2+2· (5+3) ·5/2=24+40=64 square units. This immediately shows that the shape of the figure in the right is not a rectangle.
This can be showed also by looking and the angle at vertex A. On the one hand tan A1=2/5. Hence, A1=68º11’55’’. Tan A2=3/8. Hence, A2=20º33’22’’. A1+A2=88º45’17’’.
Problem 3.
Problem 4.
``When speking of experts, the Earth, should be ruled by mathematician and physicists, since they are educated in disciplines in which it is impossible to lie.'' (Davor Pavuna, free translation from Croatian to English by me =))