Spreadsheet Data
by
Becky Mohl
I have generated several excel worksheets in order to compare several Fibonacci sequences, and see if they all go to the same limit as n gets large
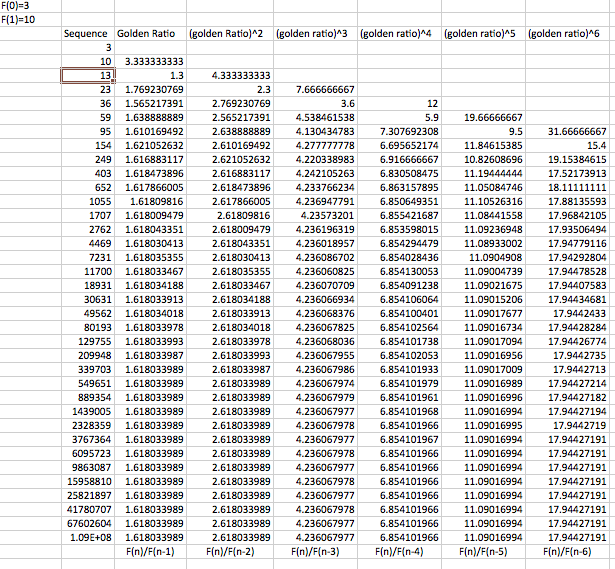
Here is a picture along with an excel spreadsheet of the Fibonacci sequence.
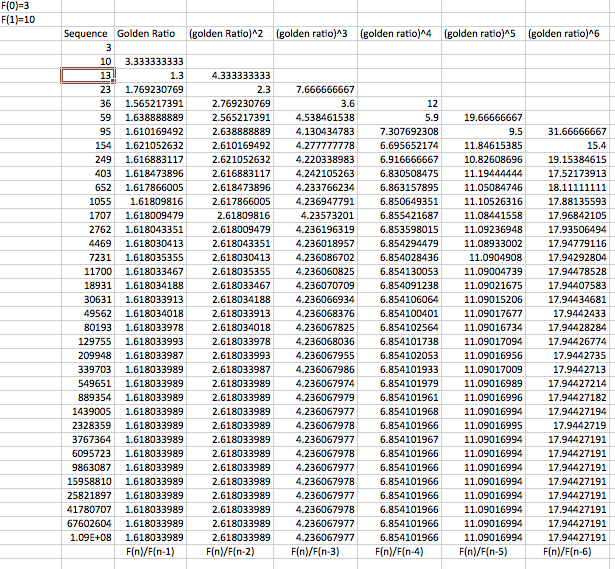
Following are several other excel worksheets comparing different sequences of the Fibonacci numbers with varying start values of F(0) and F(1).
Excel 2 F(0)=1 F(1)=3 This is called the Lucas Sequence.
After comparing all of these workbooks, I found that no matter what number we started with, F(0) and F(1), all three converged to 1.61803 as n got larger. Also, I knew that 1.61803 was equal to [(1+sqrt(5))/2] which is known as the golden ratio. So the ratios were converging to the golden ratio [(1+sqrt(5))/2].
Also if we chose to dive the two adjacent numbers, we came with another pattern. If you look at the above picture you see that the third column converges to 2.618033989. THis number is equal to the golden ration, (1.61803)^2 = 2.618033989.
A similar pattern holds true for the fourth column. Here the limit converges to 4.236067977 as n gets larger. Interested I wanted to find if this value was related to the golden ration also. I found that if you take the golden ratio, (01.61803)^3 you get 4.23067977.
This pattern continues to hold through each column. The preceding column is simply raised to the consecutive power. For example, column four is the (golden ratio)^4, and column five is the (golden ratio)^5 power.
After looking at the other workbooks, I found that the same arguments holds true in the other three not matter the start value.
Because of these several investigations, we make the assumption that any sequence of the Fibonacci numbers will always have a limit equal to the golden ratio despite the values of F(0) and F(1).
I continued to explore this matter, and found that although the values of F(0) and F(1) do make a difference in the limit of the sequence, I did find that the order of the ratios did. If we divided F(n-1)/F(n), the sequence did not converge to the golden ratio. Instead it converged to a portion of the golden ratio, .61803 which is [(1+sqrt(5))/2]-1.
Here is an excel worksheet showing that the division of the F(n-1)/F(n) does not converge to the golden ration, but a portion of it.