Product of Linear Functions

by

Becky Mohl

Find two linear functions f(x) and g(x) such that their product h(x) = f(x) * g(x) is tangent to each f(x) and g(x) at two distinct points.

Before we get to carried away with finding these two linear equations to recall what is a linear function. A linear function is any function that can be written any the form:

y = mx + b

y = nx = c

where m and n are the slope, and b and ac are the ay intercept.

Now that we remember what a linear function is, we can begin assigning numbers to m, n, b, and c. Lets think of one of the simplest linear equations. The first one that comes to mind is to let m = 1 and b = 0 as well as n =2 and c = 0. Lets take a look.

f(x) = 1x + 0 or f(x) = x

g(x) = 2x + 0 or g(x) = 2x

Now, lets consider the product of these two linear function.

h(x) = (x) * (2x) = 2x^2

Here is the graph of f(x), g(x), and h(x). f(x) is blue, g(x) is red, and h(x) is green.

Here we can see that the red and blue lines of f(x) and g(x) are not tangent to h(x); however, we do see that the product of two linear functions produces a parabola. Lets continue to explore graphs. In order to get the blue line of f(x) closer to being tangent lets try to reduce the slope of the line to m=0 instead of 1. However, if we do this, we know that slope of zero gives us a horizontal line as undefined slope gives us a vertical line. By looking at the picture, we know that neither a horizontal or vertical will give us a line that is closer to being tangent. our next option is to allow g(x) to have the same slope value with the opposite sign since we know that the slope has to be less than zero. Here are our new functions:

f(x) = x

g(x) = -2x

h(x) = (x) * (-2x) = -2x^2

Now lets look at the graph of these functions.

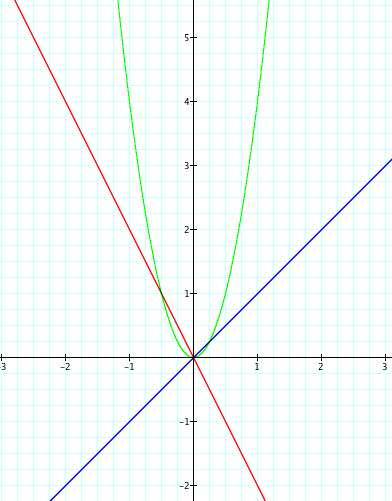
Here we see that the red line of g(x) is closer to being tangent now that it has the opposite sign of f(x). Although we are are closer to having two tangent lines, we are not there yet. We need to shift the graph until we get the two functions tangent to the product of the two functions. Since, we see that the blue line of f(x) is closer to being tangent to the parabola, lets try to divide g(x) by 2 making it have the same value of f(x) only negative. So now we have the functions.

f(x) = x

g(x) = -x

h(x) = -(x^2)

Consider the graph of these functions.

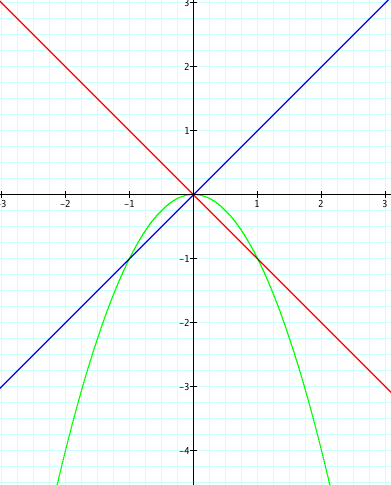
Hooray!! Now both lines f(x) and g(x) are very close to being tangent to the parabola which is the product of f(x) and g(x). Lets consider another way to spread the lines out farther. We need to move the line up some how, and we know that adding one shifts the graph up. So, lets add 1 to both f(x) and g(x) and see what the graph looks like.

f(x) = x + 1

g(x) = -x

h(x) = (x+1)(-x)

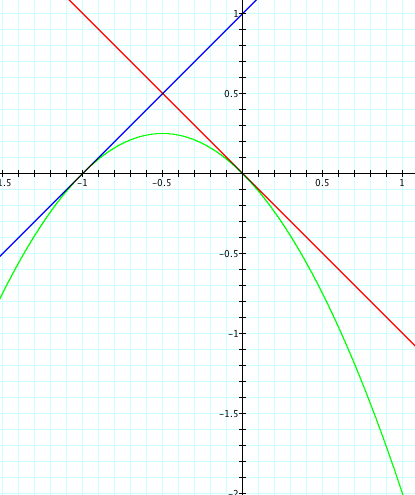
It appears that the parabola is tangent to both the red and blue lies, but we need to zoom in to make sure that they remain tangent. Upon zooming in, we are able to see that the parabola is always tangent the red and blue lines; therefore, we have shown that the product of two linear equations produces a parabola.

Back