Centers of Triangles
by
Becky Mohl
1. Centroid: The centroid is the center of the triangle construted by the intersection of a traingles three medians. A median of a triangle is a segment stretching from the vertices of a triangle to the mipoint of the opposite of the triangle. The centroid is also always inside of a triangle, no matter if it is an acute, otuse, or rigt tirangle, and always divides the triangle into equal sections.
2. Orthocenter: The orthocenter is the center of the triangle constructed by the intersection of a triangles three altitudes. An altitude of a triangle is a segment stretching from the vertices of a triangle to the opposite side. It does not go through the mipoint of the opposite side. The centroid is inside an acute triangle, outside of an obtusw trianlge and lies on a side of thr triangle when it is a right triangle.
3. Circumcenter: The circumcenter is the center of the triangle constructed by the intersection of a triangles three perpendicular bisectors. A perpendicular bisector goes throught the midpoint of the sides of the triangle dividing the segment into two equal segments; however, the perpendicular bisector does not go through the opposite vertex. The circumcenter is located inside an acute triangle, outside of an obtuse triangle, and on the side of a right triangle. In addition, the circumcenter of the triangle is equal distance from each of the vertices. Because of this the circumcenter has a circle with the circumcenter for the center and one of the vertices of the triangle as a point on the circle.
4. Incenter: The incenter is the center of the triangle constructed by the intersection of a traingles three angle bisectors. An angle bisector of a triangle bisects the angle of a triangle into tw equal halves. The incenter is always inside the triangle, and is equal distance from the sides of the trianle. The incenter also has a cicle called the incircle which has the incenter as the center and a perpendicular line stretching from the incener to the sides as the radus.
5. Use GSp to construct the centers of a triangle. What relationships do they have.
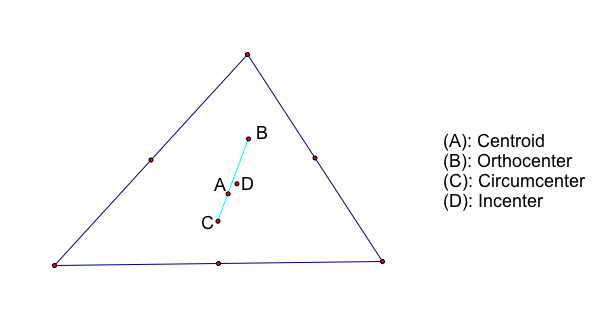
In the above picture, we see that three out of the four centers lie on the same line; however, the circumcenter does not lie on the same line.This line is known as Euler's line. Is this always true or will the circumcenter ever lie on the same line, Euler's line. as the other three centers?
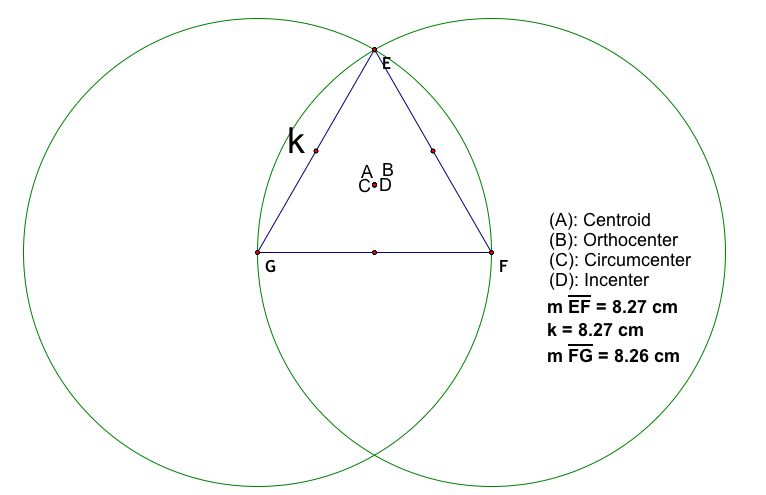
The above triangle is an equilateral triangle. Here we see that the centers all lie at the same point. Therefore, there is no line formed by the centers. So the qustion still remains, does the circumcernter ever lie on the same line formed by the other three centers.
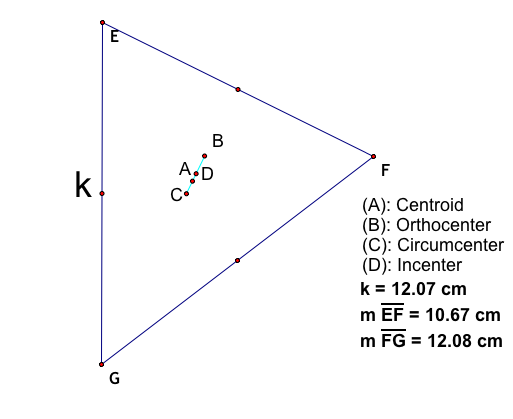
The above triangle, is an isoscles triangle and we see that the all four of the centers lie on the same line. Therefore, there is a trianlge where all four of the centers do lie on the same line, and it is an isoscles triangle. Use the GSP Animation. to move the centers around and see if you can come up with another triangle where all four centers lie on the same line.
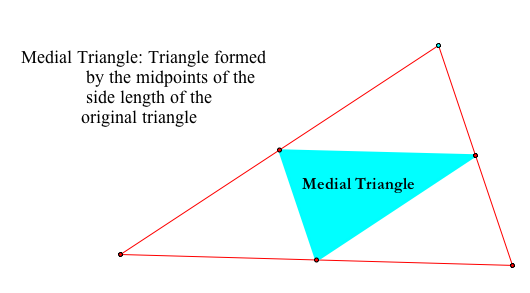
6. Medial triangle: It is the triangle formed form the centoid of the tiangle. It i similar to the original triangls, and its area is 1/4 the original triangle's area.
Now construct all four centers for both the orignial triangle, and the medial triangle. Compare the centers and Euler's line for both triangle's centers.
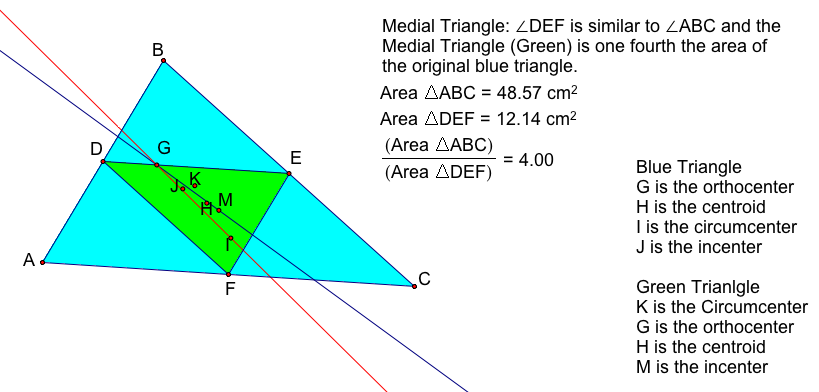
In the above picture, we see that the centers for the original blue triangle lie on the same line, and that the centers of the green medial triangle lie on a seperate line; however, the lines are not the same. Other observations include that the orthocenter of both triangle lie on both of the lines. Use the GSP Animation to see if this always holds true or if it is just a special case
7. Do the same exploration with the orthic triangle.
Orthic: It is formed by the triangle formed by the orthocenter of the triangle.
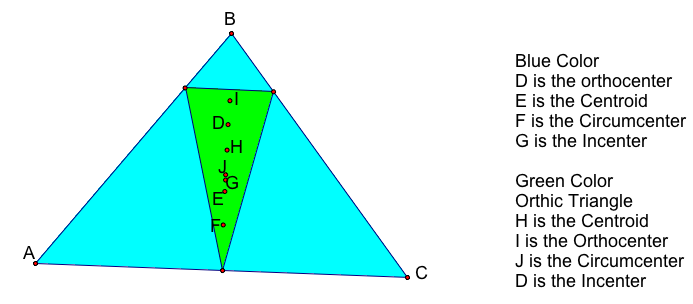
Here is a picture of the orthic center with the centers of both the original blue triangle and the green orthic triangle. Now lets compare the centers as we did in the medial triangle.
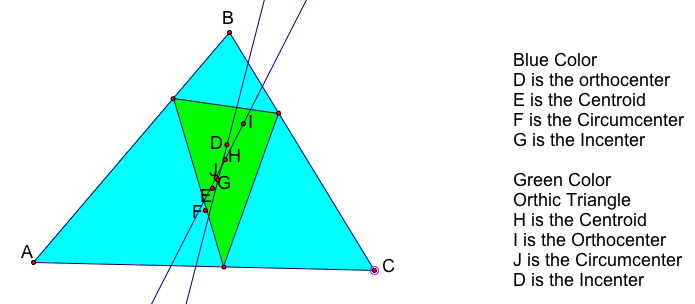
In the orthic triangle, thy centers are very close to being the same line. Use the GSP Animation to see if there is a triangle where the centers of the orthic triangle and the original triangle lie on the same line.
What relationships can you find among the four centers or subsets of them?
Below are several different animations considering different shaped triangles related to the four centers.
First lets look at the relationship between the four centers of the triangle. Animation
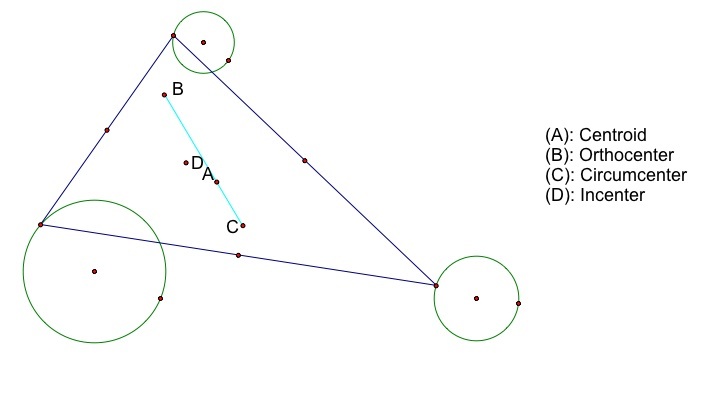
According to the above picture along with several other shaped triangle, we can say that the centroid, orthocenter, and circumcenter will always be in a straight line. Now lets consider what happens when the centers are traced.
6. Medial Triangle
7. Orthic Triangle
See if you can investigate this topic farther and see if you can come up with proofs as to why these constructions work!
Back









