Tangent Circles

by

Becky Mohl

 

Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point. First we draw two circles where one circle is inside the other. In addition, draw the radius of the small circle as a segment between the two given point, the center and a point on the circle.

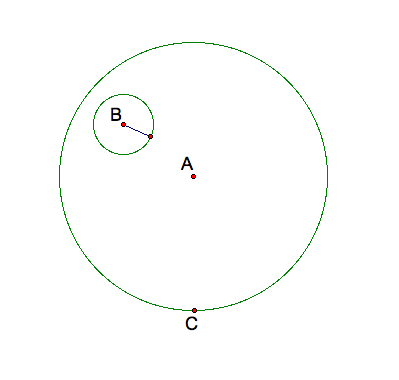
Next, draw a line that passes through the center of the large circle and point C which is on on the large circle. Now construct a line passing through point B and C. Mark the intersections between lines AC and BC as D. Then construct a circle at center C and use the radius of the small circle to construct the circle CD.

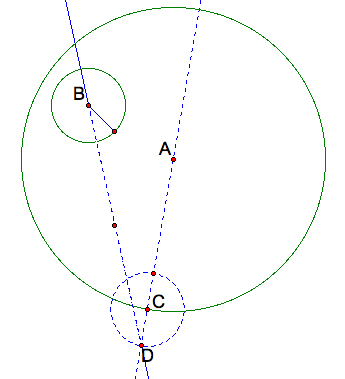
After constructing the new circle CD (blue), construct the segments AD and BC. Next construct the midpoints of segment BD, and then construct a perpendicular line with through the midpoint. Construct and label the intersection with segment AC as E.

Finally, construct a segment EC. Let E be the center and EC the radius, and construct a circle by center and radius. This circle (red), should be tangent to both the original green circles.

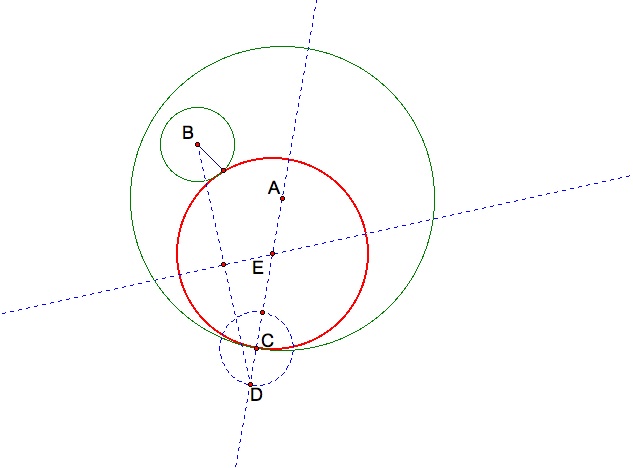
Here is a construction in GSP including a script tool for constructing a tangent circle to a circle within a circle. Animation 1.

Next, lets look at what happens when we are given two circles that intersect at two points. How do we construct a tangent circle? Use the same construction as above to find the tangent circle to the two intersecting green circles which were given. In order to do this we can use the script tool in GSP to recreate the construction and move the circle to intersection instead of one inside the other.

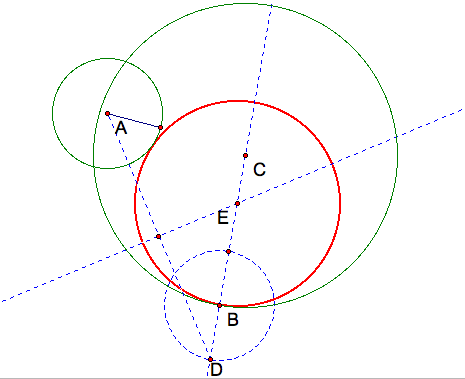
Here above, we see that the construction does appear to be the same as the previous constructions. Use the GSP Animation to explore different shapes. I found that as the circle centered at point A gets bigger, the tangent red circle gets smaller. Can you find other observations? One other interesting I found is if we trace the points above. If we trace point E, and animate point B, lets see what happens as point B moves around the larger circle. In order to make the ellipse, we need to first make the locus. The definition of a locus for the ellipse is that an ellipse is a curve that is the locus of all points in the plane, the sum of two distances r1 and r2 from to fixed points F1 and F2 (the foci) departed by a distance of 2c is a given positive.

So, in our picture the foci are points A and E.

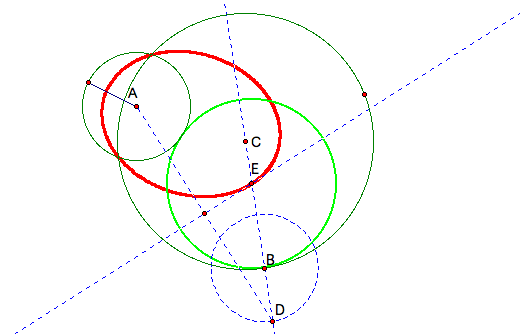
Above, we see that the trace created an ellipse (red). Animation. The green circle is still the tangent circle between the tow disjoint circles.

Let's see what we create when we have two disjoint circles. Again select point E to trace and point B to animate. The definition of a locus for a hyperbola is that the locus of all points P in the plane, the difference of whose distances from tow fixed points the foci separated by a distance of 2c. Again our foci for the hyperbola are A and E.

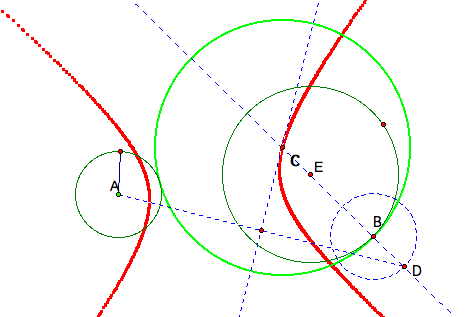
Above, we see that the trace created a hyperbola (red). Animation . The green circle is still the tangent circle between the two disjoint circles.

 

 

Back