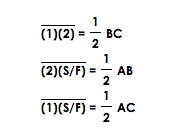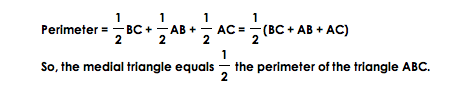Bouncing Barney
by
Becky Mohl
Barney is in a triangular room. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns abd walks parallel to AB. Prove that Barney will eventually return to his starting point. How many times will Barney reach a wall befre returning to his starting point? Explore and discuss for various starting points on line BC, including points exterior to segment BC. Discuss and prove any mathematical conjectures you find in the situation.
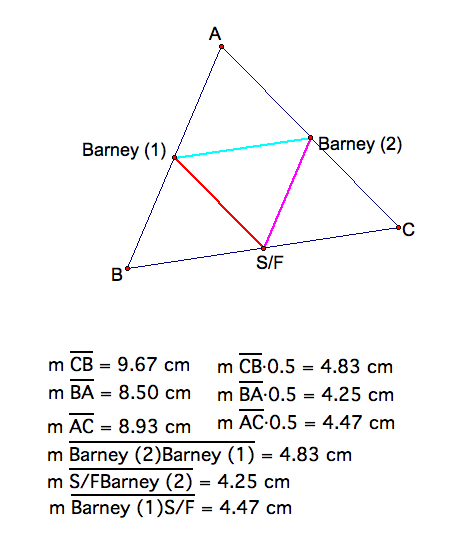
Here is the room that Barney is in and the path that he must travel. However. we need to see how the path changes as we chang his starting point S/F on BC.
Animation
In order to consider various starting poits, let's separate each unique situation in cases.
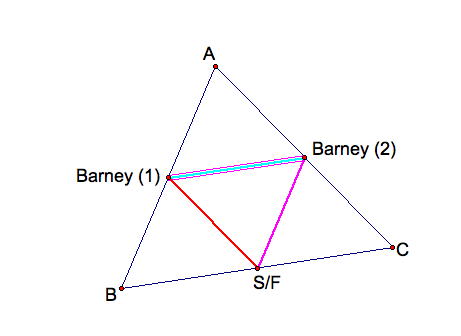
Case 1: Let Barney's starting point be the midpoint of BC, S/F.
In this case, when we trace Barney's path, we get the followind design.
After constructing Barney's path from midpoint to midpoint, I realized that the path made a triangle, but what kind of triangle. Then I remembered that a triangle that goes through all three midpoins of each side of the triangle is called the medial triangle. Therefore, the triangle (S/F)(1)(2) is the medial triangle of ABC. In addition, I know that we can draw the midesegments of each side which is a segment that connects the midpoint of two sides. Let's see what it would look like.
Proof that Barney will return to the midpoint of BC.
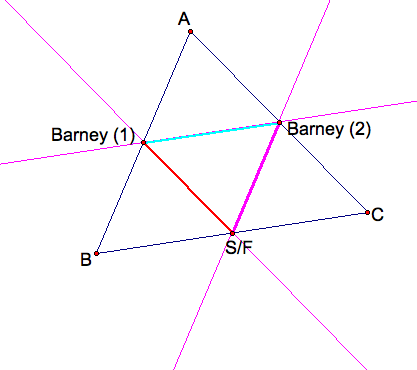
Here we can see some more parallel lines. We know that the midesegment, (1)(2) is parallel to BC, and the midsegment (1)(S/F) is parallel to AC, and the midsegment (2)(S/F) is parallel to AB. By prperties of midsegments since all three midsegments are parallel to the third side of the triangle. we know that that the midsegment is half the third side's length. This means that midsegment (1)(2) = .5 BC, (2)(S/F) = .5 AB, and midsegment (1)(S.F) = .5 AC.
Therfore, Barney traveled a length half as long as the perimeter. Also, by starting at the midpoint of BC, Barney only hit each wall one time. So, he made three hits total.
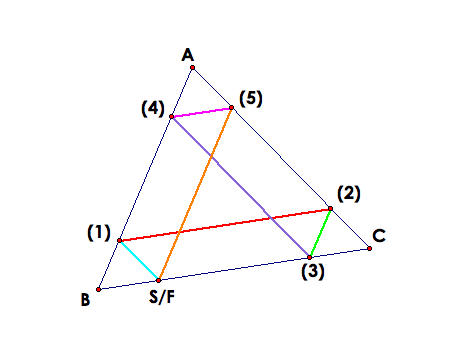
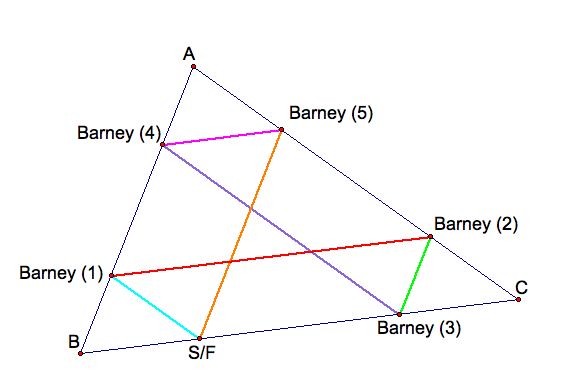
Case 2: What if Barney did not start on the midpoint of BC?
Instead of assuming that Barney comes back to the same point, let's assume he does not. Therefore, construct a triangle and a path where S anf F are not equal, and proof that they have to be equal. Here is the picture we will use.
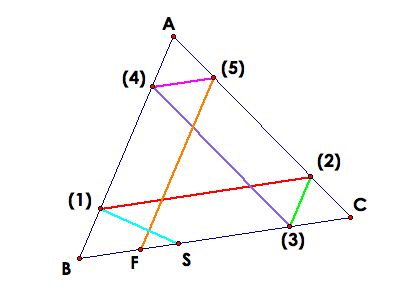Animation
Again we know that if a line is parallel to a side of the triangle and goes through the other two sides, then the the line divides the side into two equal segments. Therefore,
This means that point F must equal point C whi means that Barney did in fact return back to his original starting point, S, after hitting each wall twice. Therefore, he made six hits in all.
In addition we know that all of the triangles made by Barney's path are all similar due to the fact that all of the lines that were constructed are parallel line. By definition of parallel lines, we know that a transversal, which is a line connectint opposite sides of the parallel lines makes the alternate interior angles equal. Then by similarity, we know that correspoinding angles are equal, and corresponding sides are proportional.
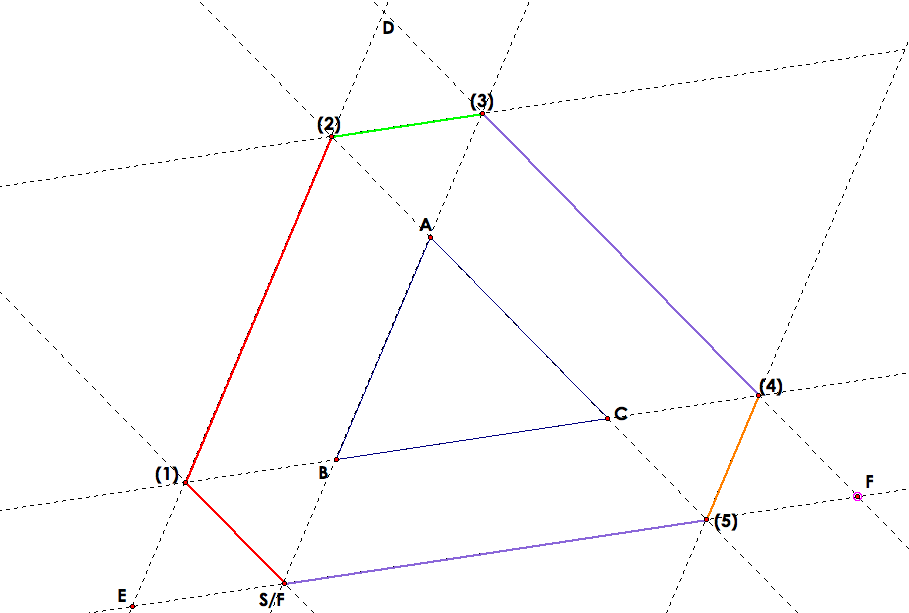
Case 3: What happens if Barney starts outside the triangle ABC, but still on BC?
Proof that Barney returns back to his starting point
Since DF is parallel to AC and EF is parallel to BC, then triangle DFE is similar to BCA..
Sine ED is parallel to AB and DF is parallel to AC, then the triangle EDF is similar to BAC.
SInce EF is parallel to BC and DF is parallel to AC, then triangle DEF is similar to ABC.
Finally since these points lie on the similar triangles, Barney's path must start and end at the same point.