

Investigation of Centers of Triangles
By
Moni Olubuyide
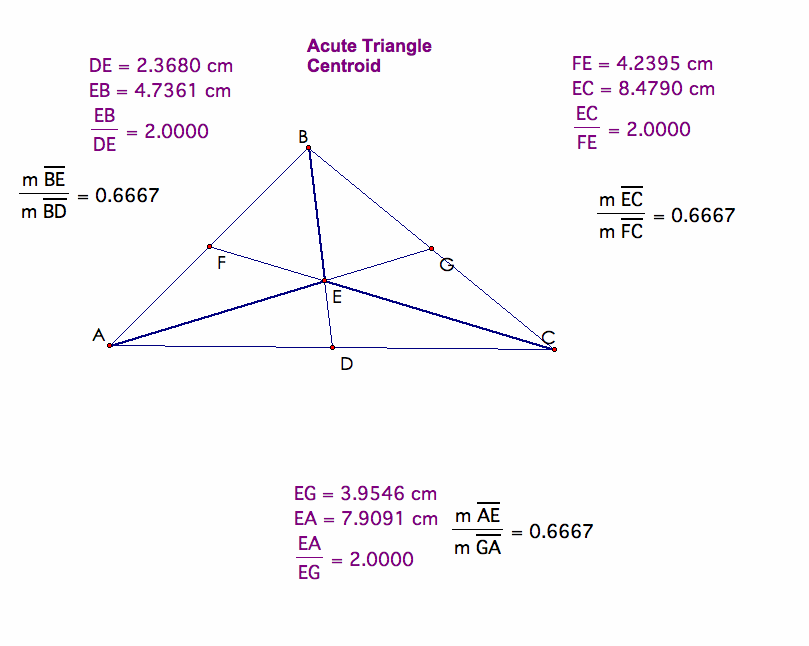
The most common center of a triangle is the centroid. The centroid is like the center of gravity of a triangle. Let's explore
CLICK HERE FOR ANIMATION OF CENTROID
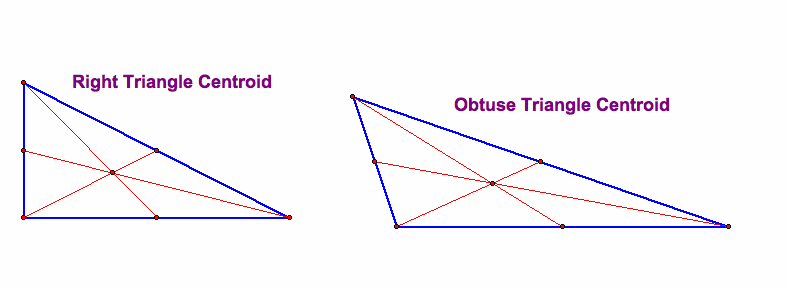
Notice that the distance from the median to the vertex is 2/3 of the length of the median. Secondly, the ratio of the distance from the vertex to the centroid compared to the centroid to the base of the median is 2:1. Another aspect of the centroid is that despite the type of triangle it will always be inside of the triangle....observe for yourself...
Now let's investigate another center of a triangle...the orthocenter. The orthocenter is the intersection of 3 lines containing the altitudes of the vertices of a triangle.
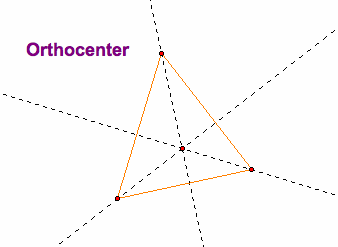
Notice that in an acute triangle the orthocenter lies inside of the triangle...
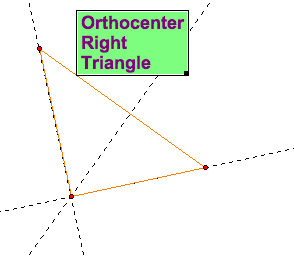
In a right triangle, the orthocenter is at a vertex of the triangle!! The side of a right triangle containing the right angle is also its altitude so it makes sense for the orthocenter to be at the vertex of this triangle....
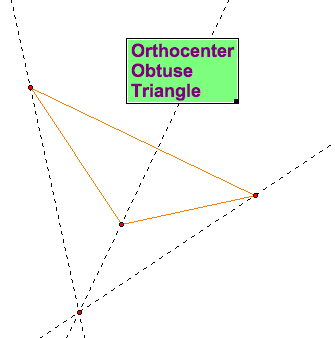
In an obtuse triangle, the ortocenter is outside of the triangle!!! Unlike the centroid, the ortocenter moves freely depending on the type of triangle....