Assignment 11

Polar Equations

Kathy Radford

 

  

   
EMAT 6680
Assignment 11
Making Beautiful Flowers Using Polar Equations of Trigonometric Functions and Graphing Calculator in 3 Steps
 
 
Step1
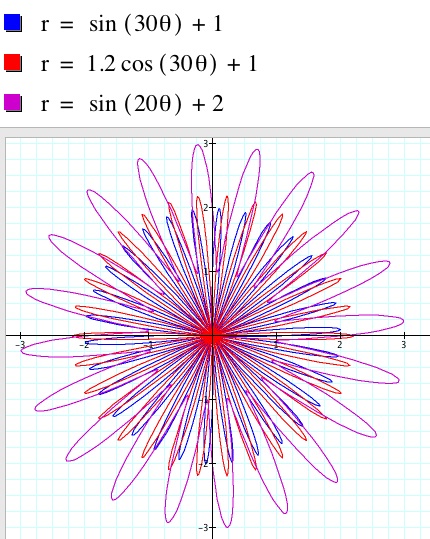
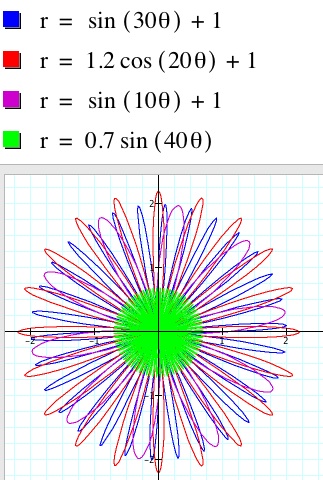
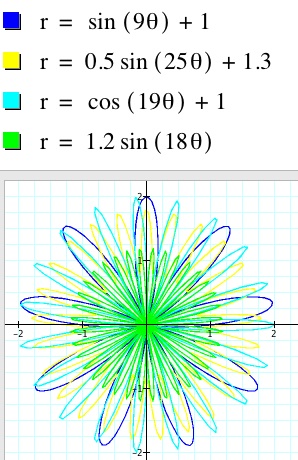
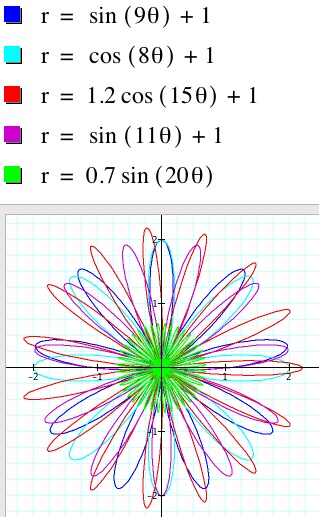
We will use equations of the form r = a (sin (k q)) + b, and r = a ( cos (k q)) + b
As can be seen from the graph below, the only difference between using sine and cosine is a 90 degree phase shift.  The length of the petals is determined by the amplitude a, k is the number of petals in one circumference of the flower, and b will move the petals out or in on the flower.
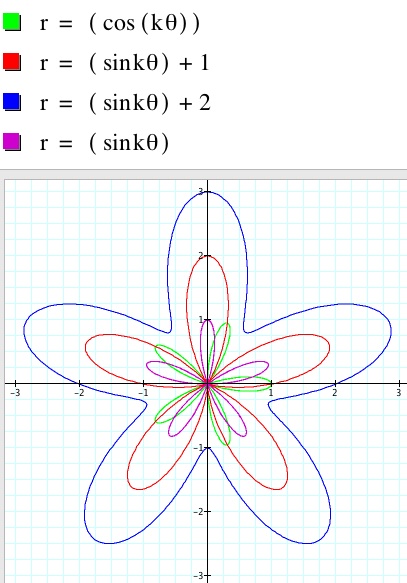
We will start with 2 basic functions to start:

 
 
 
Step 2
Setting k = 5 produces 5 petals.  Adding 1 keeps the sine function from ever being negative, while adding 2 moves it even farther from the origin.  Using a cosine rotates the graph by p/2. 
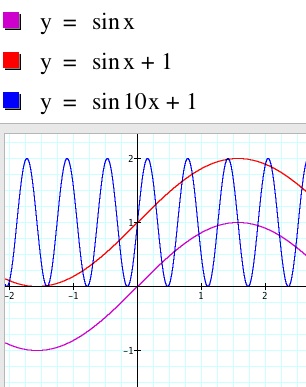
The “flower”  is actually the result of taking a sine function such as the one shown below in purple,  adding a constant to make all values positive (red), and increasing the frequency by k to make extra “petals” (blue), and “wrapping” it into a circle.
 

 

 
 
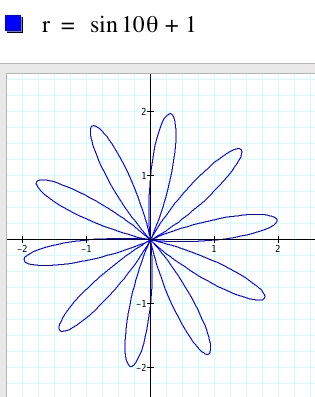
Step 3
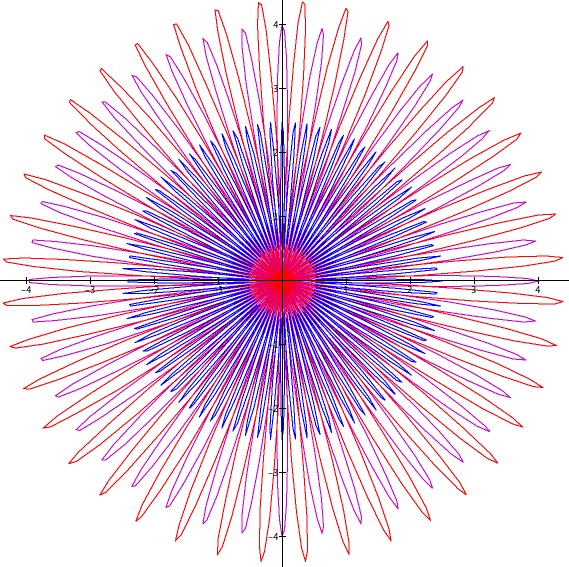
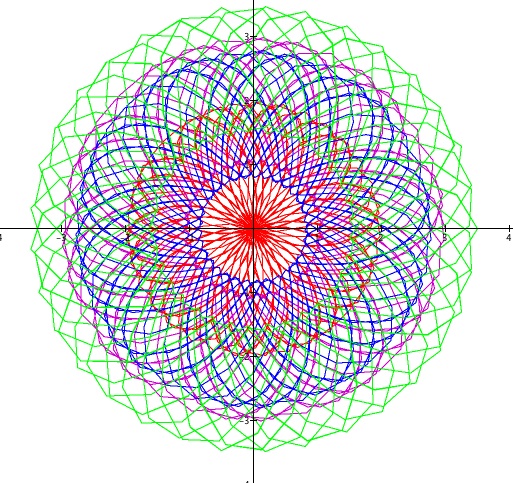
By layering different values for the amplitude a, frequency k, and radial shift b, and changing colors, many beautiful flowers can be produced.