The Nine-Point Circle was investigated by French and German mathematicians in the early 1800s.

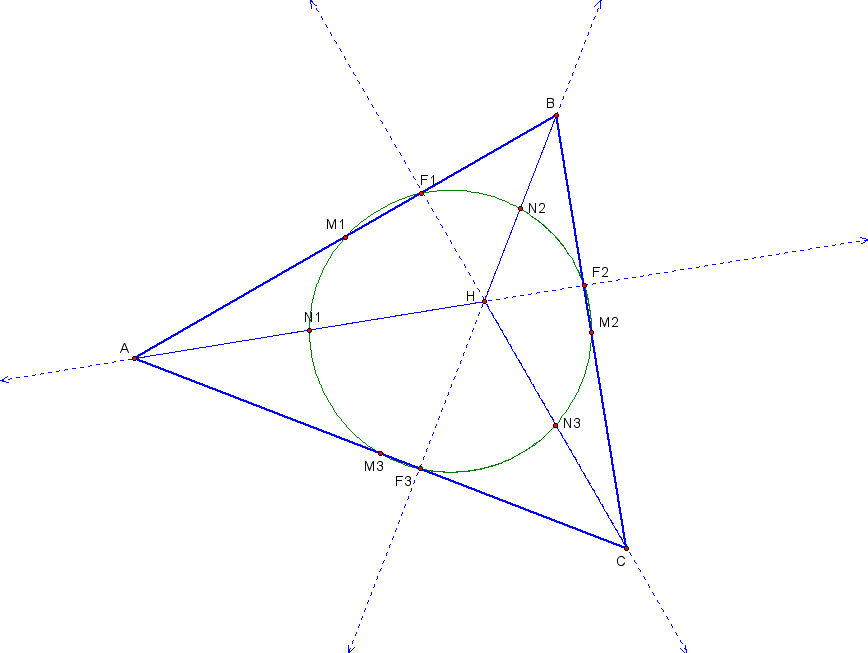
There are nine particular points associated with any triangle that form the nine point circle. Starting with a triangle ABC, we will construct these points and show that they all lie on one circle - the Nine-Point Circle.

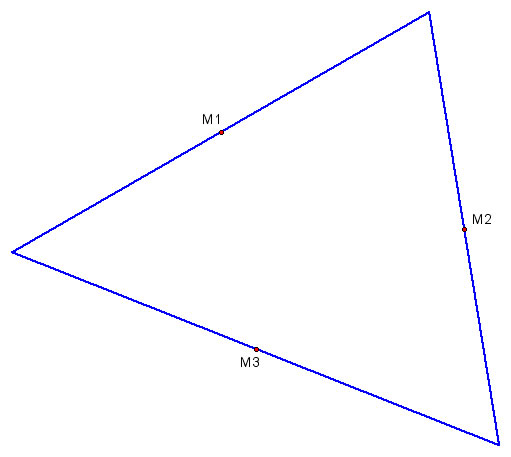
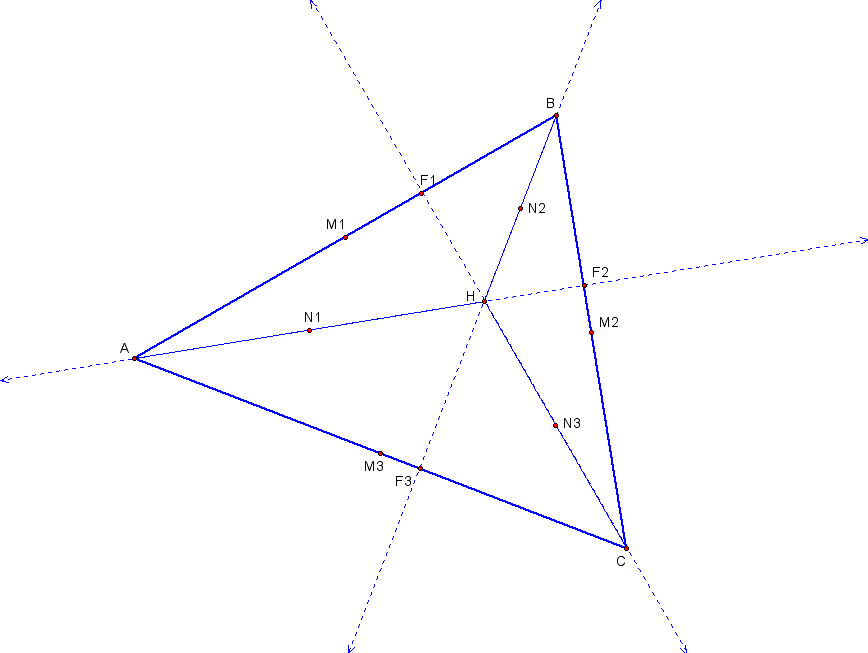
1) Starting with triangle ABC, we will construct the midpoints of the three sides, and name them M1, M2, and M3, as shown below:

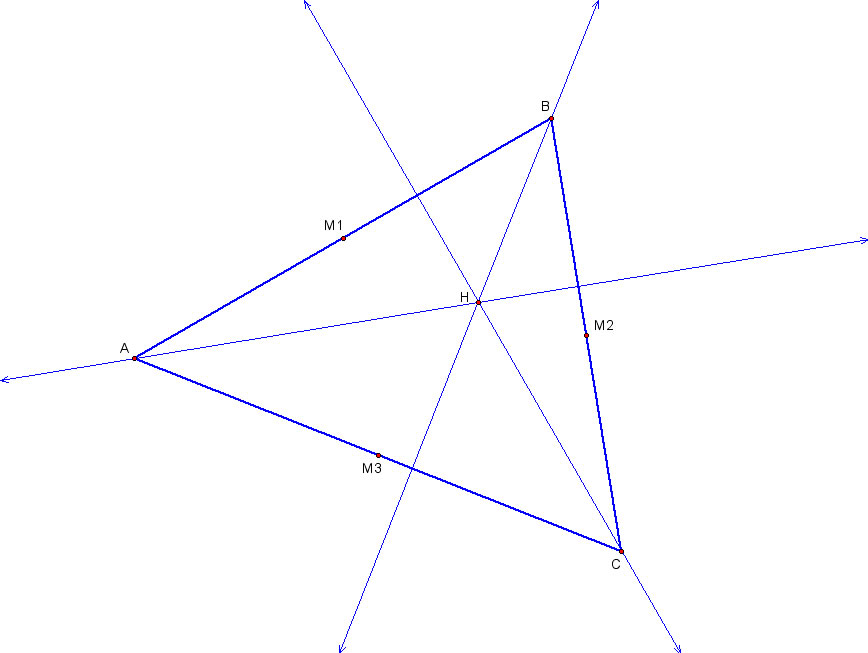
2) Next, we will find the point H, the orthocenter, which is the intersection of the three altitudes of the triangle:

3) We now construct segments from H to the vertices A, B, and C of the triangles, and find their midpoints, N1, N2, and N3.

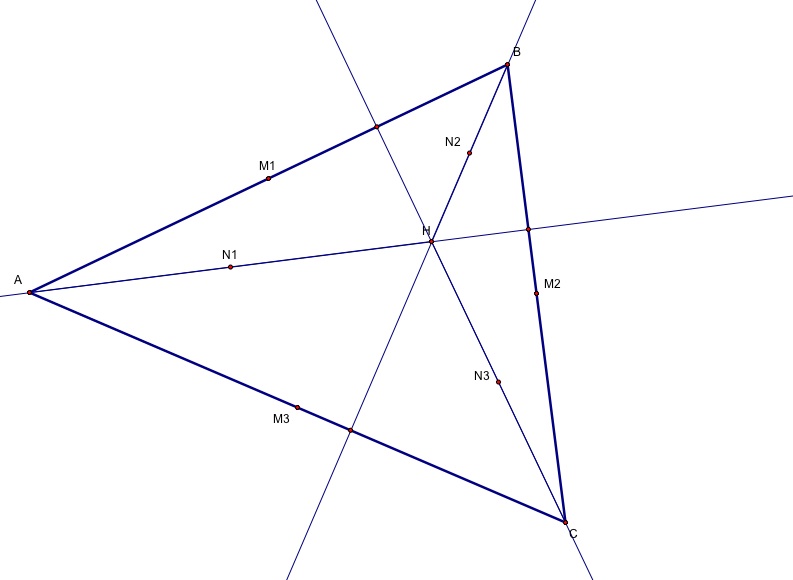
4) The last three points are the "feet" of the altitudes - the points of intersection of the altitudes with the sides of the triangle. We will label them F1, F2, and F3.

5) We can find the center of the nine point circle by constructing a triangle from any three points, and finding the circumcenter - the point of concurrency of the perpendicular bisectors, as shown below:

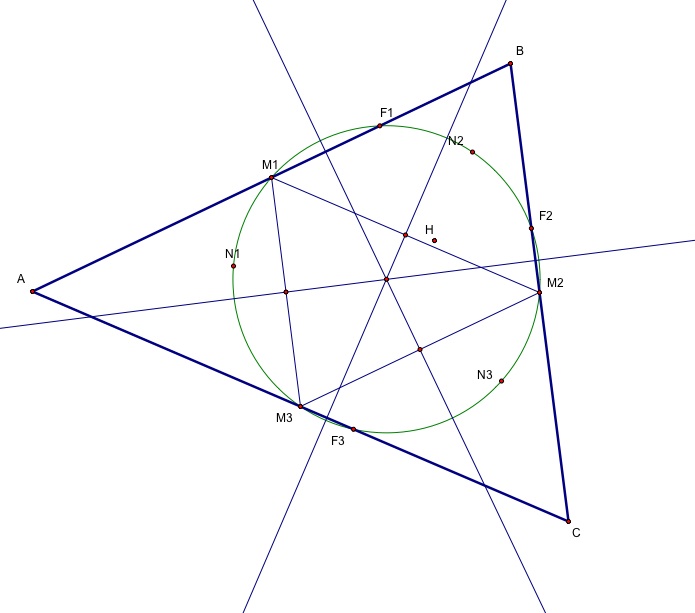
6) Now we have the nine points in place, and can show the circle.