
Quadratic Equations Solved Geometrically
by Jackie Ruff
The
ancient Greek mathematicians did not have the algebra upon which we
rely so heavily today. But that did not stop them from reasoning out
solutions for quadratic equations. Their solutions relied on area
models and on the use of proportions. This method is not commonly
included in the curriculum of American high schools today, but with the
popularity of using manipulatives to teach mathematics, maybe it should
be considered. If emphasizing geometry is not in vogue for its
own sake, it could certainly be used to illustrate and add meaning to
our symbols and algebraic manipulations.
In his book, A Survey of Geometry, Howard Eves lists a series of questions to lead the reader through geometric solutions of quadratic equations, but does not provide solutions. His first suggestion is to consider the relationship of the coefficient of x and the constant term in a quadratic equation.
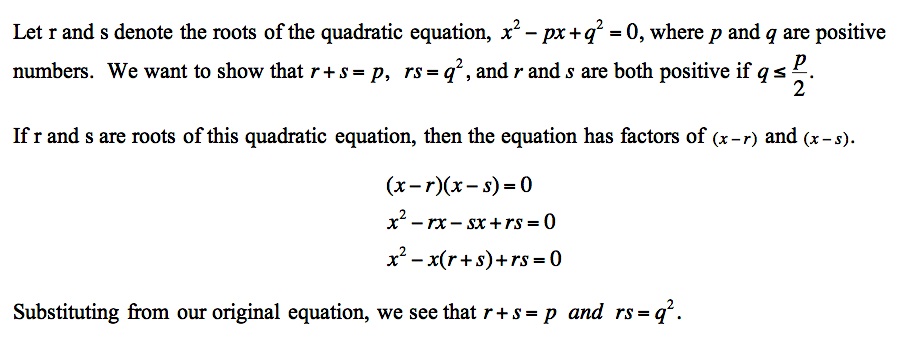
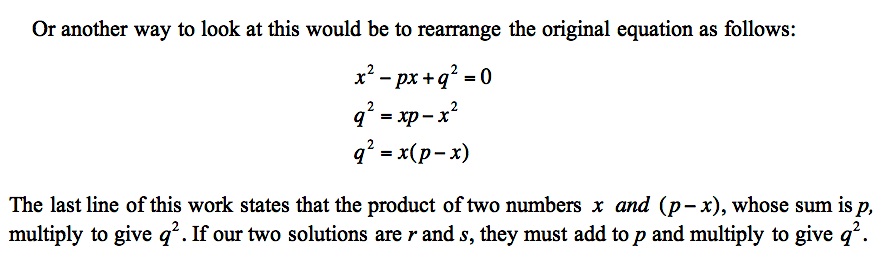
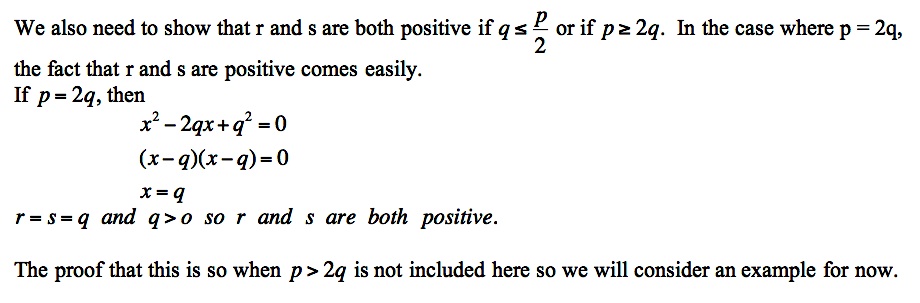
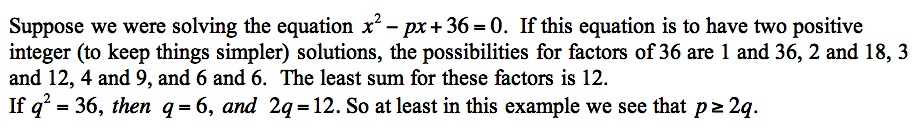



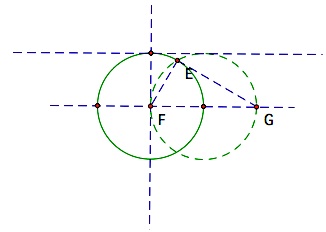
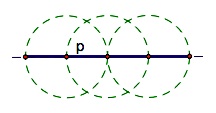
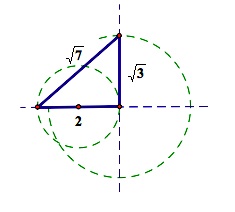
To accomplish
this we will construct a circle with diameter of p so that we can easily
construct a right triangle with an altitude of q.
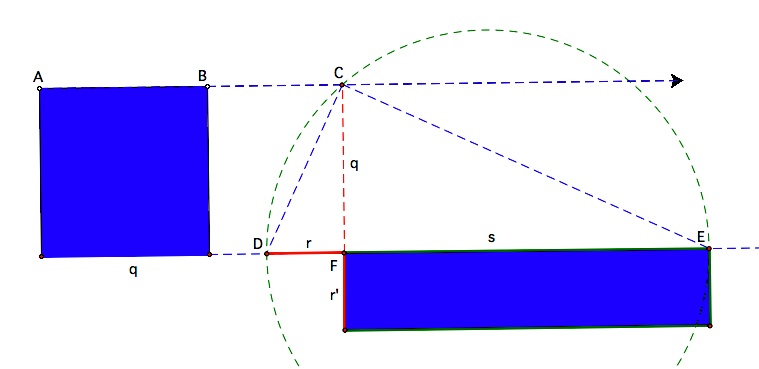
Earlier we were to show that for r and s to be positive, q must be less than or equal to half of p. Another look at the diagram above shows that since the radius of the circle is p/2, a value of q greater than that would not intersect the circle. This means there would be no solution where r and s add to p.

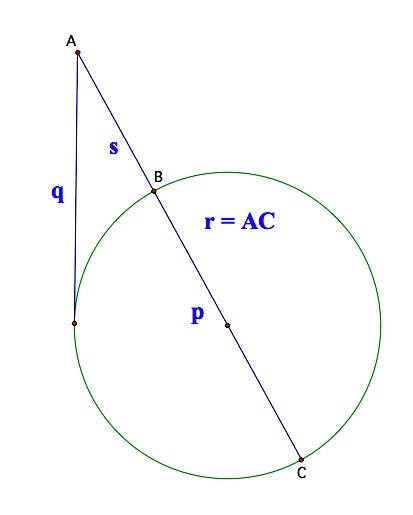
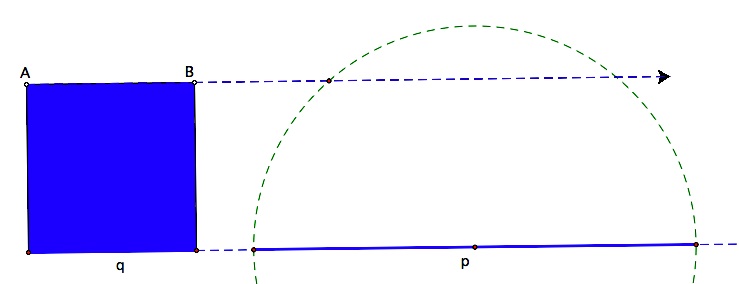
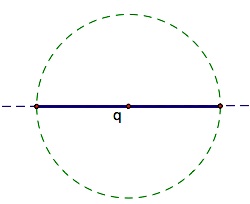
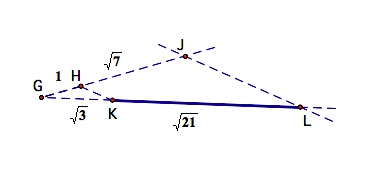
So, we need to construct a circle with a diameter of p, and then construct a tangent to that circle of length q. That will locate point A and determine the length of the segment s. These tasks are performed in the sequence of diagrams below.
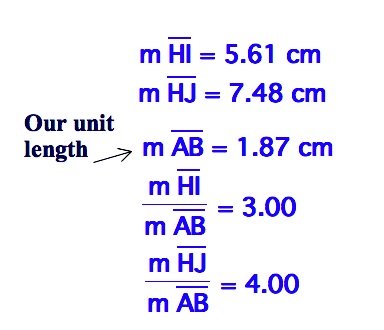
Next we will solve a couple of specific quadratic equations using these methods. To work with the given values in our equation, we will need to specify a unit of length.
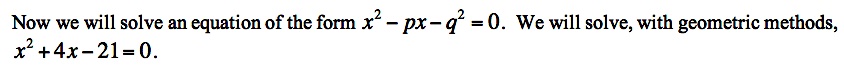
ReferencesIn his book, A Survey of Geometry, Howard Eves lists a series of questions to lead the reader through geometric solutions of quadratic equations, but does not provide solutions. His first suggestion is to consider the relationship of the coefficient of x and the constant term in a quadratic equation.
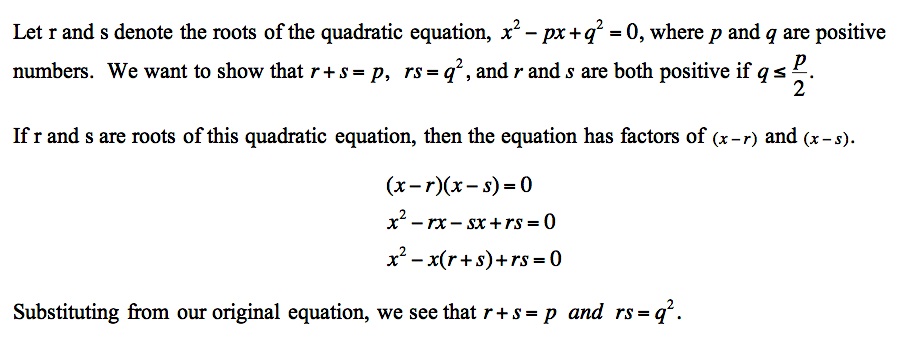
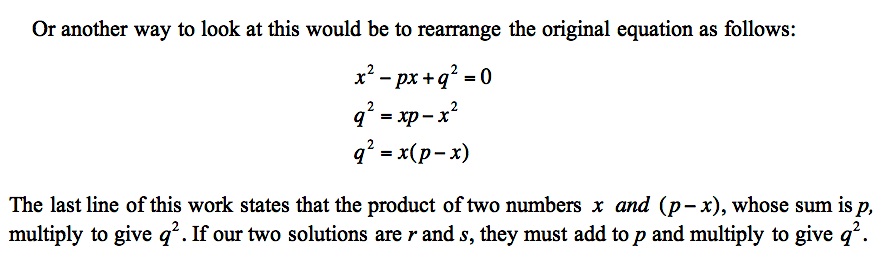



construct a right triangle with an altitude of q.
 |  |
 |  |
 |  |
 |  |

The construction to solve this equation is based on a diagram in Eves' book (p. 24) similar to the one below.

So, we need to construct a circle with a diameter of p, and then construct a tangent to that circle of length q. That will locate point A and determine the length of the segment s. These tasks are performed in the sequence of diagrams below.
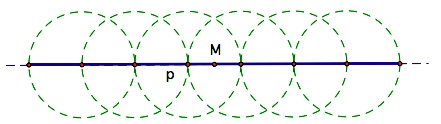
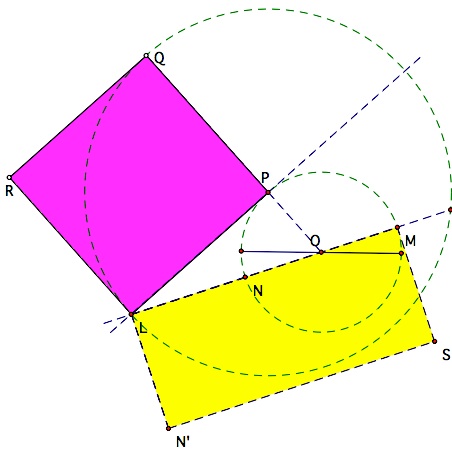
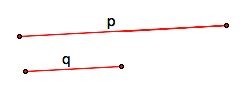 Given two segments of length p and q. | 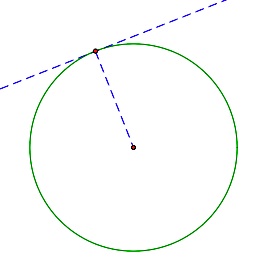 Construct a tangent to a circle with diameter p and, in the diagram to the right, a circle at the point of tangency with a radius of q. | 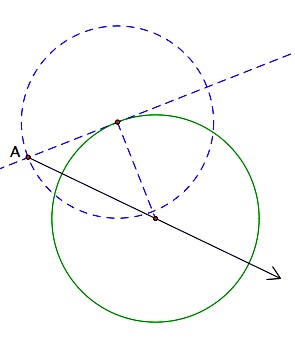 | 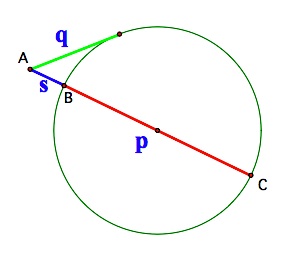 Construct a line through A and the center of the circle to locate points B and C. |
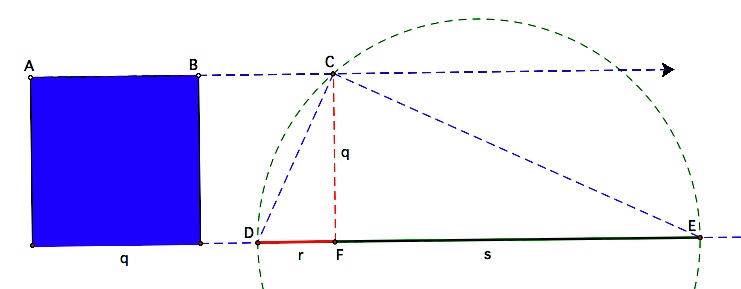
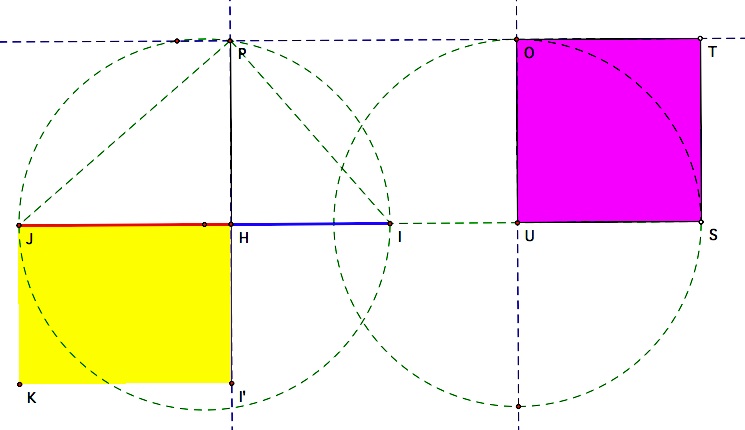
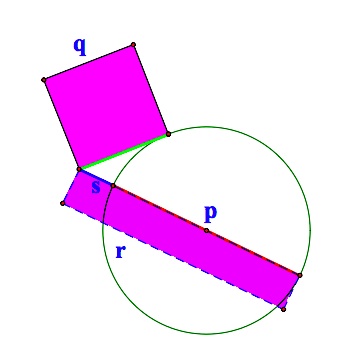 We have constructed the segments r and s, the lengths of which have a difference of p. To show that the area of the rectangle equals the area of the square, we need another theorem. If the line containing a chord and a tangent intersect at point A outside a circle, then the product of the distance from A to one endpoint of the chord (r) and the distance to the other endpoint (s) 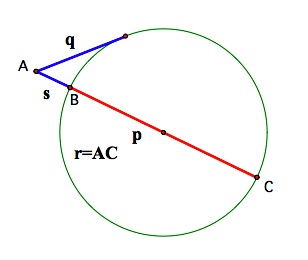 equals the square of the length of the tangent segment (q). So, equals the square of the length of the tangent segment (q). So, 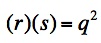 .For a proof of this theorem, see this Geometer's Sketchpad file. .For a proof of this theorem, see this Geometer's Sketchpad file. | |||
Next we will solve a couple of specific quadratic equations using these methods. To work with the given values in our equation, we will need to specify a unit of length.
 |  | |
 | ||
 |  |  |
 |  |  |
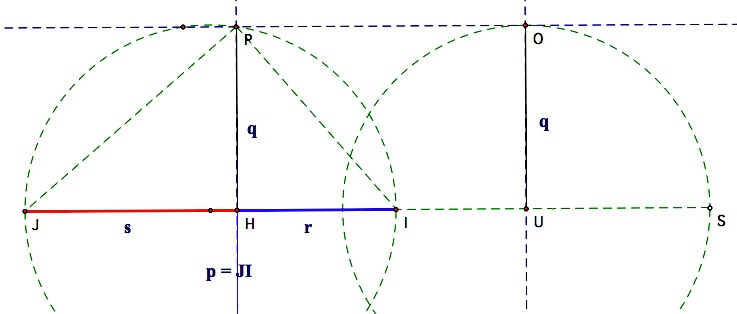 | Finally after building all of these lengths, we can construct a right triangle in the circle at the far left with an altitude of q. This divides the diameter (p) into segments of length r and s whose lengths are the solutions to our equation. | |
 |  | |
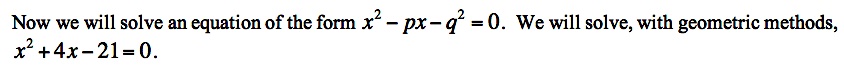
  | ||
  |  | |
  |  | |
 |   | |
Eells, W. (1911). Greek Methods of Solving Quadratic Equations. The American Mathematical Monthly, 18(1), 3-14.
Eves, H. (1963). A Survey of Geometry. Boston: Allyn and Bacon, Inc.
Hornsby, E. (1990). Geometrical and Graphical Solutions of Quadratic Equations. The College Mathematics Journal, 21(5), 362-369.
Libeskind, S. (2008). Euclidean and Transformational Geometry, A Deductive Inquiry. Boston: Jones and Bartlett
Eves, H. (1963). A Survey of Geometry. Boston: Allyn and Bacon, Inc.
Hornsby, E. (1990). Geometrical and Graphical Solutions of Quadratic Equations. The College Mathematics Journal, 21(5), 362-369.
Libeskind, S. (2008). Euclidean and Transformational Geometry, A Deductive Inquiry. Boston: Jones and Bartlett