Using Spreadsheets to Explore Loans and Compound Interest
by
Jackie Ruff
If
you have invested money in a savings account that pays compound
interest, that means that you will earn interest on the interest that
you earn - which sounds good!
To understand the formula that we could use to see how much money you will have in an account after a certain amount of time, let's watch your money grow for a few months.
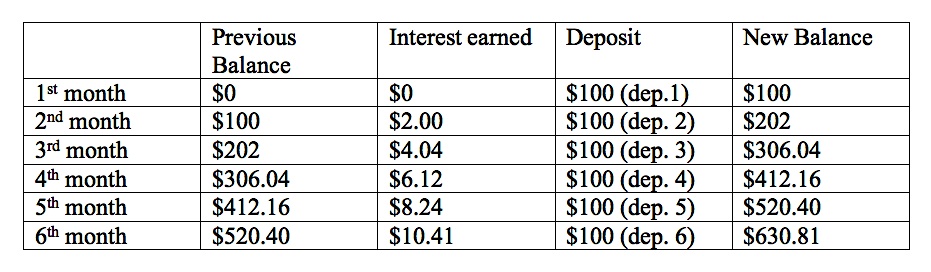
Suppose you invest money at the rate of $100 per month and earn 2% interest (hopefully you would earn more than that but we are keeping it simple) every month. Let's follow your money for 6 months.
At the end of the first month, you deposit $100.
At the end of the second month, your first $100 has been in the bank for 1 month, so the bank adds 2% to your account. What is 2% of $100?
Yes, that is an easy one - $2. So, now you have a grand total of $102. Then it is your turn to deposit another $100 into your account, so you have $202. Let's put this in a table so we can keep up with everything better.
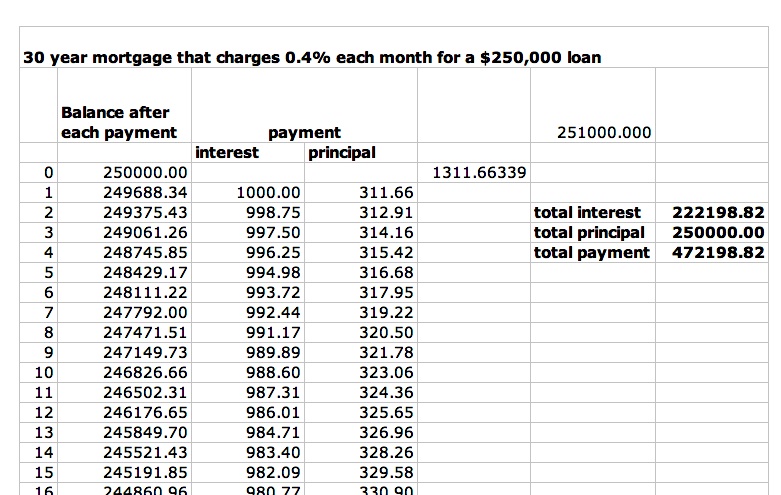
Recall that our initial plan is to pay off a loan of $250,000 at 0.4% interest over 30 years. Below is a portion of a spreadsheet where the monthly payment was calculated using the formula that we just obtained above.
If you would rather see the entire spreadsheet, click here for an Excel file and look at tab 1.
Since the 1st payment is not made until the end of the month, the original loan amount has already climbed to $251,000. By the end of 30 years, you will have paid, $472,198.82 for the house - about 189% of what you borrowed! But, the plus side is that you were able to live in the house for those 30 years, too.
Now, your 0.4% monthly interest rate is equivalent to 12(0.4%) = 4.8% annual interest. Suppose you have the opportunity, about 8 years into this loan, to refinance. There are two options available - a 20 year loan at 4% APR, or a 15 year loan at 3.8% APR. Let's compare.
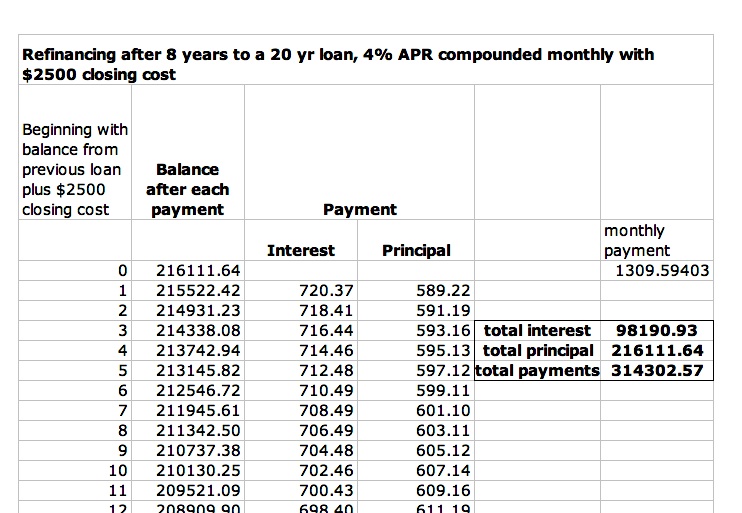
Below is a partial spreadsheet for the 20 year loan beginning with the remaining balance owed after 8 years of payments. Again, you may click here for the spreadsheet and look at tab 2.
The monthly payment is about the same as before, but you could save a lot of money overall!
Let's look at the 15 year option.
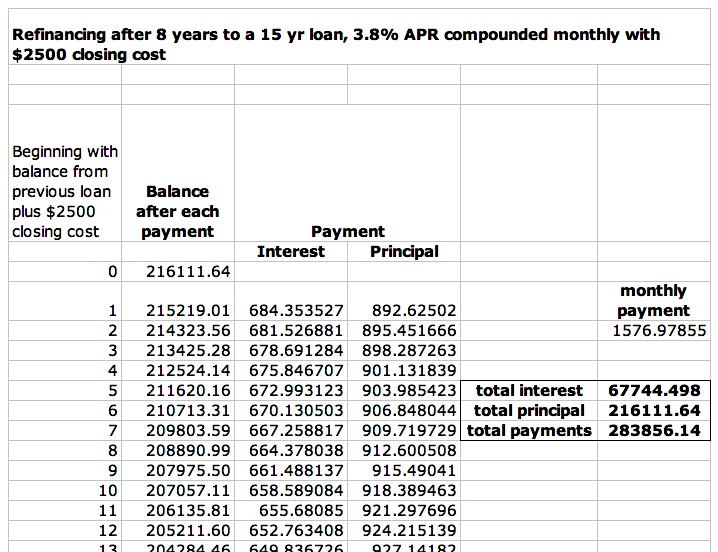
Here, we would save even more! But look at the payment - can you afford that every month?
If we look at a graph, we can certainly look forward to completing these loan payments early.
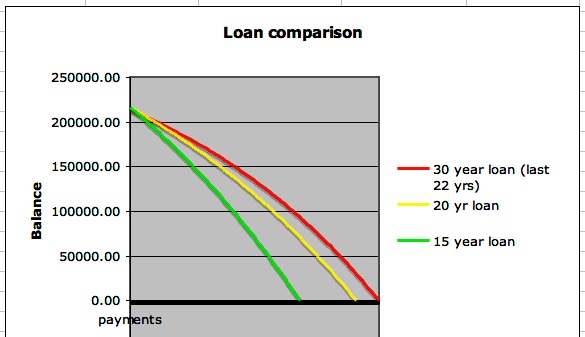
But we should compare the numbers carefully before we decide. Look at the summary below:
To understand the formula that we could use to see how much money you will have in an account after a certain amount of time, let's watch your money grow for a few months.
Suppose you invest money at the rate of $100 per month and earn 2% interest (hopefully you would earn more than that but we are keeping it simple) every month. Let's follow your money for 6 months.
At the end of the first month, you deposit $100.
At the end of the second month, your first $100 has been in the bank for 1 month, so the bank adds 2% to your account. What is 2% of $100?
Yes, that is an easy one - $2. So, now you have a grand total of $102. Then it is your turn to deposit another $100 into your account, so you have $202. Let's put this in a table so we can keep up with everything better.
Look at the interest column. The $2.00 was interest paid on deposit 1.
The $4.04 was interest paid on deposit 1 and on deposit 2 (plus the earned interest).
The $6.12 was interest paid on deposits 1, 2, and 3 (plus the earned interest).
The $8.24 was interest paid on deposits 1, 2, 3, and 4 (plus interest).
The $10.41 was interest paid on deposits 1, 2, 3, 4, and 5. The final deposit has earned no interest at this point.
How many times has that first $100 investment earned interest?
Did you count that it was 5 times in 6 months?
How about each of the other deposits?
If you figured out the pattern, the following formula may make sense. We are using A for the amount of money in the bank after 6 months and D for the deposit amount. We will use i for the monthly interest rate and N for the number of months. As you read equation 1, look at the balances in the table from the bottom to the top.
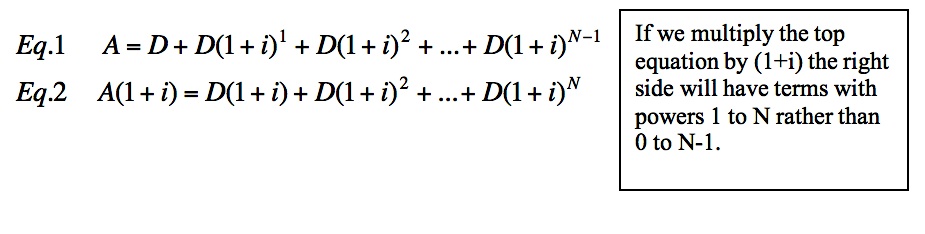
You should try this formula with the information from the problem above to confirm that it gives you the same number as our final balance in the table.
When deciding on a loan for a large purchase such as a car or a house, several factors would influence our decision. Even though it would cost us less to borrow the money for a shorter period of time, we cannot plan to make monthly payments that we cannot afford. So, we must balance what we can comfortably pay every month with a loan that costs us as little as possible over the years.
Let's consider borrowing money for a $250,000 house with an initial plan to take 30 years to repay at 0.4% interest each month.
We need another formula to figure out what we would need to pay every month to get this done in 30 years.
We know two formulas to find the future amount of money where compound interest is involved.
First,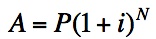
is
the compound interest formula (compounded monthly) where P is the
principal, i is the monthly interest rate, and N is the number of
months.
And we have the formula we used earlier that involves the amount of monthly payment, D,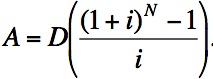
.
Since both of these formulas equal A, we will set them equal to each other and try to solve for D, which will be our monthly payment in this case, rather than a deposit into a savings account.
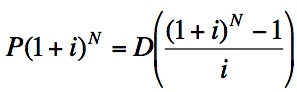We need to solve for D, so we multiply both sides by the reciprocal of the fraction on the right.
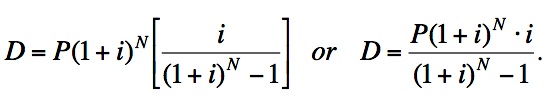
We will simplify this last equation by dividing both the numerator and denominator by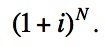
We then have,
, where i is the monthly rate and N is the number of months.
Since most banks and loan companies state interest rates as APR (annual percentage rate), we will substitute
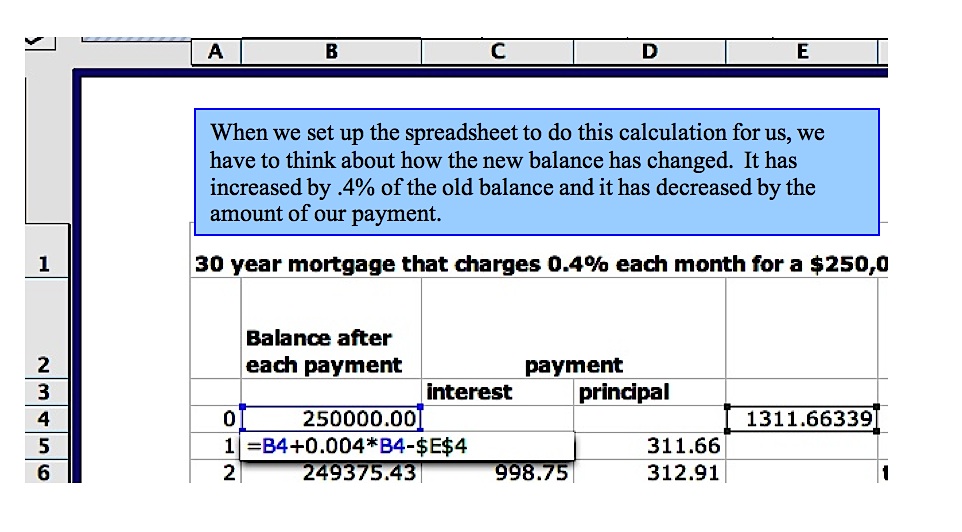
Even though the spreadsheet will do the work, we have to tell it what to do. Look at the portion of a spreadsheet below and think about the formula used to obtain the new balance after each payment. It would help to work through a few steps of the table manually.
The $4.04 was interest paid on deposit 1 and on deposit 2 (plus the earned interest).
The $6.12 was interest paid on deposits 1, 2, and 3 (plus the earned interest).
The $8.24 was interest paid on deposits 1, 2, 3, and 4 (plus interest).
The $10.41 was interest paid on deposits 1, 2, 3, 4, and 5. The final deposit has earned no interest at this point.
How many times has that first $100 investment earned interest?
Did you count that it was 5 times in 6 months?
How about each of the other deposits?
If you figured out the pattern, the following formula may make sense. We are using A for the amount of money in the bank after 6 months and D for the deposit amount. We will use i for the monthly interest rate and N for the number of months. As you read equation 1, look at the balances in the table from the bottom to the top.
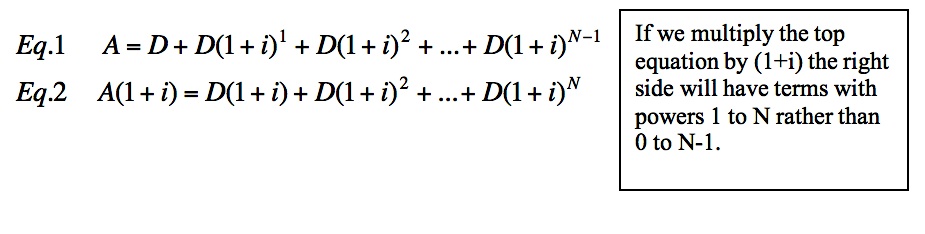
You should try this formula with the information from the problem above to confirm that it gives you the same number as our final balance in the table.
When deciding on a loan for a large purchase such as a car or a house, several factors would influence our decision. Even though it would cost us less to borrow the money for a shorter period of time, we cannot plan to make monthly payments that we cannot afford. So, we must balance what we can comfortably pay every month with a loan that costs us as little as possible over the years.
Let's consider borrowing money for a $250,000 house with an initial plan to take 30 years to repay at 0.4% interest each month.
We need another formula to figure out what we would need to pay every month to get this done in 30 years.
We know two formulas to find the future amount of money where compound interest is involved.
First,
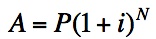is
the compound interest formula (compounded monthly) where P is the
principal, i is the monthly interest rate, and N is the number of
months.And we have the formula we used earlier that involves the amount of monthly payment, D,
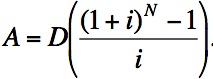.Since both of these formulas equal A, we will set them equal to each other and try to solve for D, which will be our monthly payment in this case, rather than a deposit into a savings account.
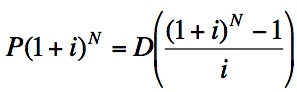We need to solve for D, so we multiply both sides by the reciprocal of the fraction on the right.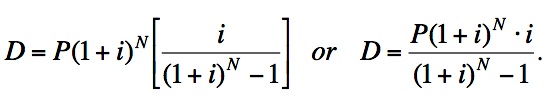We will simplify this last equation by dividing both the numerator and denominator by
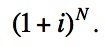
We then have,
, where i is the monthly rate and N is the number of months.Since most banks and loan companies state interest rates as APR (annual percentage rate), we will substitute
Even though the spreadsheet will do the work, we have to tell it what to do. Look at the portion of a spreadsheet below and think about the formula used to obtain the new balance after each payment. It would help to work through a few steps of the table manually.
Recall that our initial plan is to pay off a loan of $250,000 at 0.4% interest over 30 years. Below is a portion of a spreadsheet where the monthly payment was calculated using the formula that we just obtained above.
If you would rather see the entire spreadsheet, click here for an Excel file and look at tab 1.
Since the 1st payment is not made until the end of the month, the original loan amount has already climbed to $251,000. By the end of 30 years, you will have paid, $472,198.82 for the house - about 189% of what you borrowed! But, the plus side is that you were able to live in the house for those 30 years, too.
Now, your 0.4% monthly interest rate is equivalent to 12(0.4%) = 4.8% annual interest. Suppose you have the opportunity, about 8 years into this loan, to refinance. There are two options available - a 20 year loan at 4% APR, or a 15 year loan at 3.8% APR. Let's compare.
Below is a partial spreadsheet for the 20 year loan beginning with the remaining balance owed after 8 years of payments. Again, you may click here for the spreadsheet and look at tab 2.
The monthly payment is about the same as before, but you could save a lot of money overall!
Let's look at the 15 year option.
Here, we would save even more! But look at the payment - can you afford that every month?
If we look at a graph, we can certainly look forward to completing these loan payments early.
But we should compare the numbers carefully before we decide. Look at the summary below:
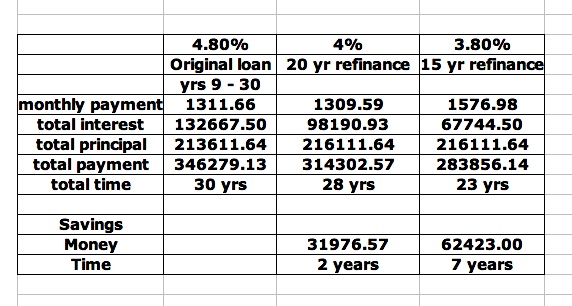 | If
the 20 year plan were our only option, we should refinance without
question. The monthly payment is actually less and we finish 2
years early! However, if we could afford the additional $267.39 every month, look what we could save with the 15 year plan. Now that we've done our homework - it's time to go to the bank. |