Further Investigation of equations of the form ax2 + bx + c = y

by

Jackie Ruff



Let's begin this investigation by looking at a group of parabolas, y = x2 + bx + 1.  Look at the set of graphs below paying attention to the path that the vertices are taking.

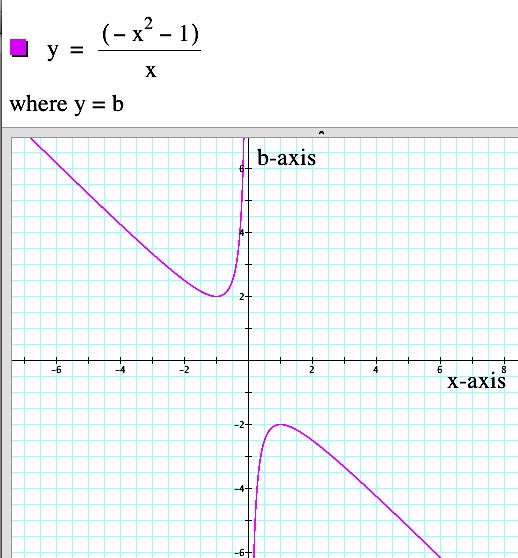
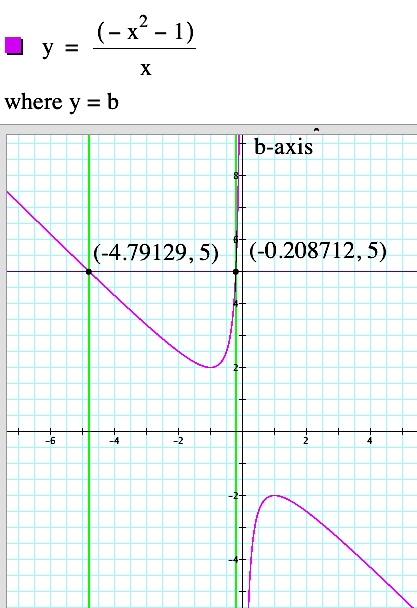
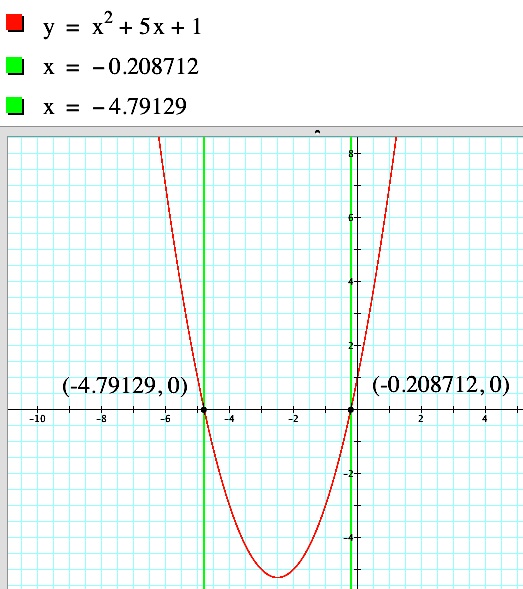
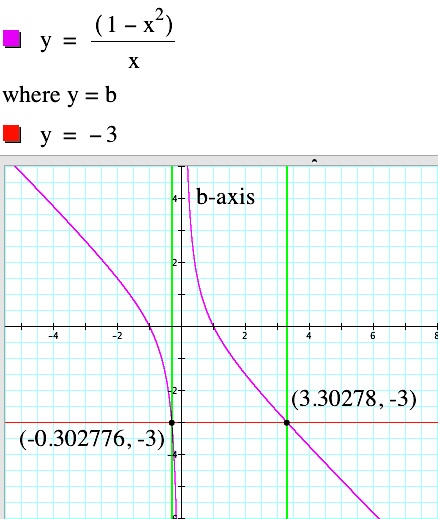
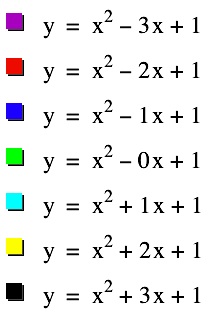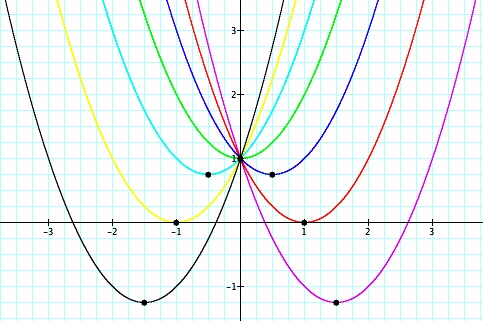parabola equationsparabola graphIt appears that the vertices are also following the path of a parabola, opening downward with a vertex at (0,1).

A3text1text2part1text2part2

If we graph this equation with our group of parabolas, it appears that we have found the correct equation.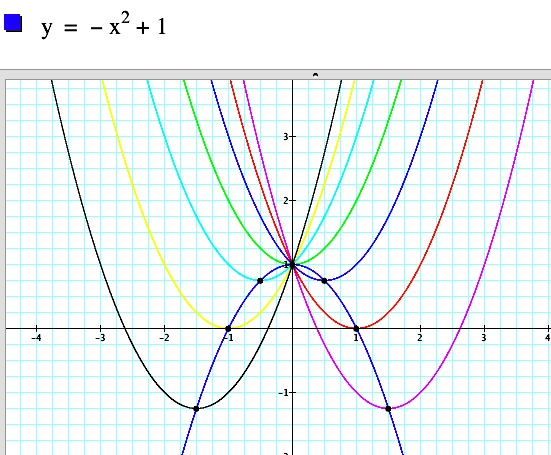vertexparab

We could confirm our results by finding the equation another way.  If we select three of the vertices and find the quadratic equation through those points, we find the same equation.  To see the work, click here.



Part 2:
Next we will consider the equation x2 + bx + 1 =0. We want to see what looking at the graph in the xb plane will tell us.

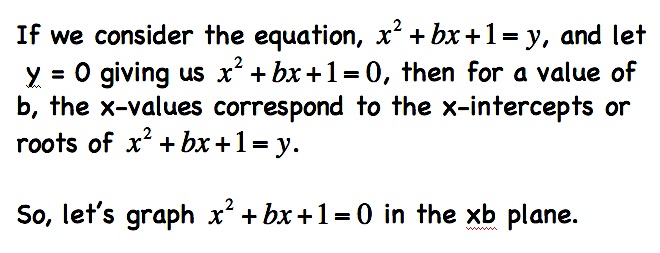part2text1A3xbplane1.jpg

part2text2A3xbplane2A3xbplane

So, now we see that we can find the roots of any of a group of quadratic equations, by graphing in the xb plane and looking at the x-values for a particular value of b. We can also see for which values of b that group of equations has one or two real roots and when it has only imaginary roots.

So, let's look at one more example now that we know what to look for.

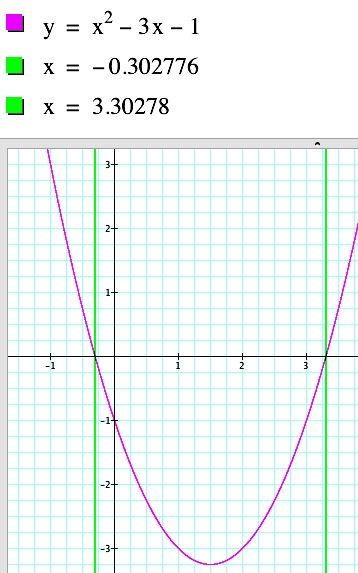part2text3A3xbplane4A3xbplane5