
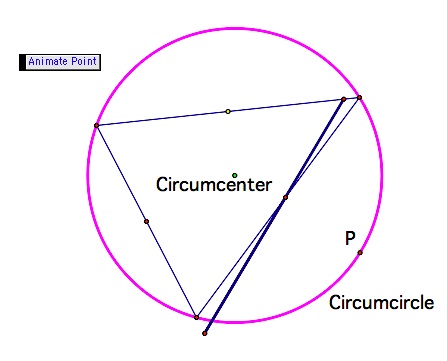
Pedal Triangles - Some Observations
by Jackie Ruff
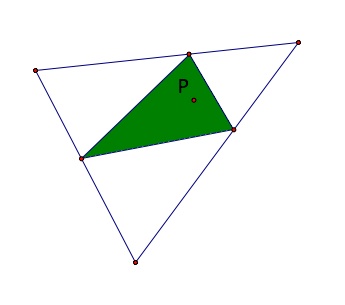
A
pedal triangle is formed when perpendicular lines are drawn to the
sides of a given triangle from a point in the plane. The points
of intersection are the vertices of the pedal triangle. See the
diagram below and then open the Geometer's Sketchpad file to see the
various positions of the pedal triangle as the pedal point moves and to
create your own pedal triangles using the script tool.
If the pedal point is on the circumcircle of the triangle, the pedal triangle degenerates to a line, known as the Simson line.
 |  | 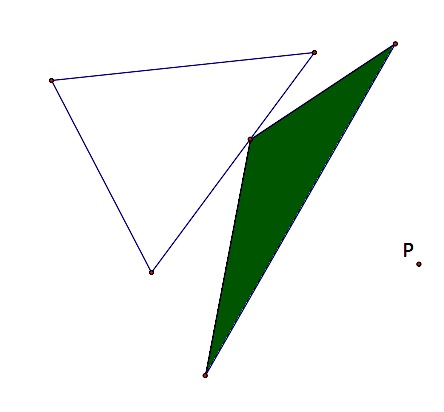 |
If the pedal point is on the circumcircle of the triangle, the pedal triangle degenerates to a line, known as the Simson line.

We
can see in the diagram to the left that when the pedal point is on the
circumcircle, the points that would be the feet of the perpendiculars
become collinear. If we look at the diagram below, we can see all of
the perpendicular lines involved. There is also a GSP file to watch an animation as the pedal point moves around the circumcircle.

Now, let's move the pedal point to the center of the circumcircle and see what we find.
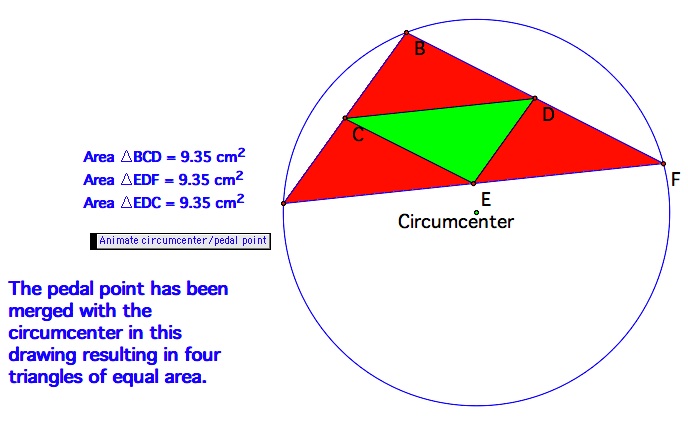
In this drawing the pedal point is labeled as circumcenter. Open this GSP file and watch the animation to see if the areas of the triangles remain the same as the pedal point moves.
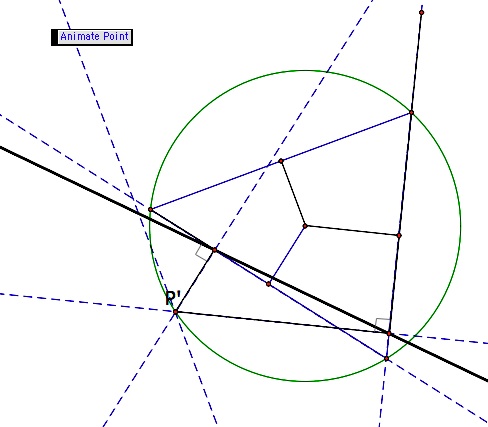
Let's look at one more interesting property of these pedal triangles. If we locate the midpoints of the sides of the pedal triangle and trace their paths as the pedal point moves, we find that they move in elliptical paths.
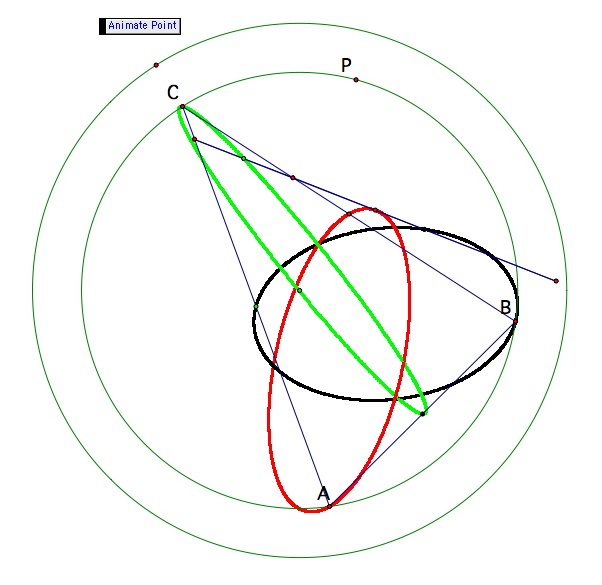
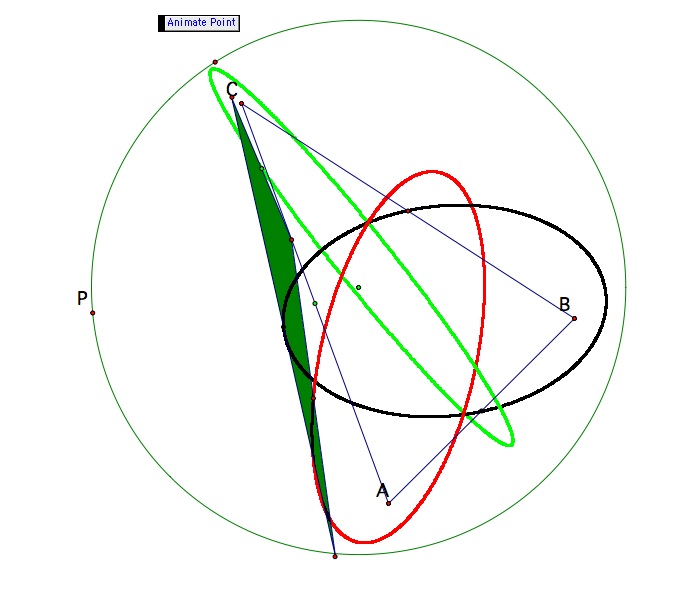
In the first diagram, the pedal point is on the circumcircle, so the pedal triangle is a line. Note that each ellipse goes through a vertex and the midpoint of the opposite side. In the diagram below, the pedal point has moved around a circle with a larger radius (so we have a pedal triangle again).

In this drawing the pedal point is labeled as circumcenter. Open this GSP file and watch the animation to see if the areas of the triangles remain the same as the pedal point moves.
Let's look at one more interesting property of these pedal triangles. If we locate the midpoints of the sides of the pedal triangle and trace their paths as the pedal point moves, we find that they move in elliptical paths.

In the first diagram, the pedal point is on the circumcircle, so the pedal triangle is a line. Note that each ellipse goes through a vertex and the midpoint of the opposite side. In the diagram below, the pedal point has moved around a circle with a larger radius (so we have a pedal triangle again).

Open this GSP file to make some ellipses for yourself.