We are going to use Geometer's Sketchpad to investigate properties of medians.

First, let's construct a triangle and its medians.  We remember that the medians connect each vertex to the midpoint of the opposite side.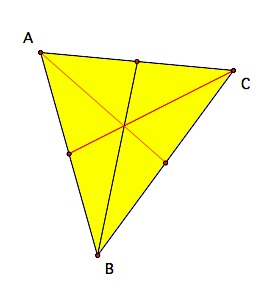

By using the measuring tools in GSP, we see a situation where the areas of the two triangles formed when a median is constructed have the same measure. Click on this link to open a GSP file with an animation to see if this happens with other triangles.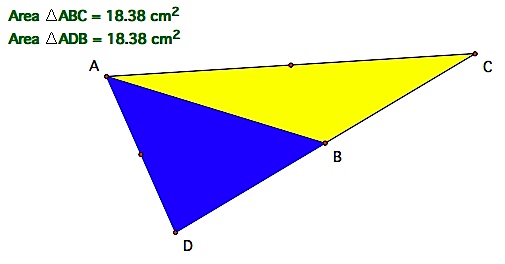
Of course the animation doesn't prove anything.  So, we will see if we can prove that a median divides a triangle into two equal areas.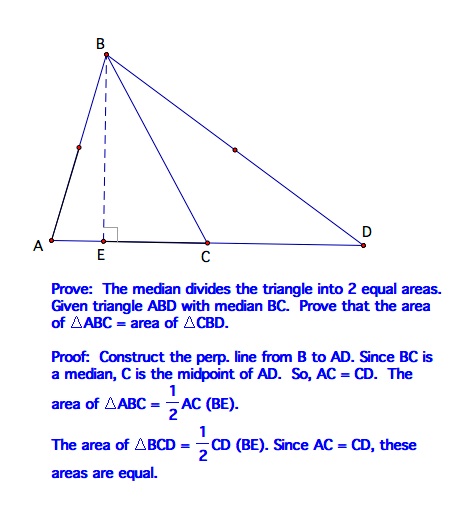

If we want to investigate medians further, we could construct a second triangle using the medians of the first as the sides of the second triangle to see if there is a relationship between the original and second triangles. In this Geometer's Sketchpad file, triangle EFG has sides the lengths of the medians of triangle ABC.  As point A moves changing the size and shape of that triangle, we can see that the ratio of the areas of the two triangles remains constant.  Now, we just have to prove it.

 

Trying to look at the two triangles separately and prove the relationship between their two areas seems difficult.  So, we will try constructing the 2nd triangle attached to the first triangle. The construction instructions and the proof are given below.
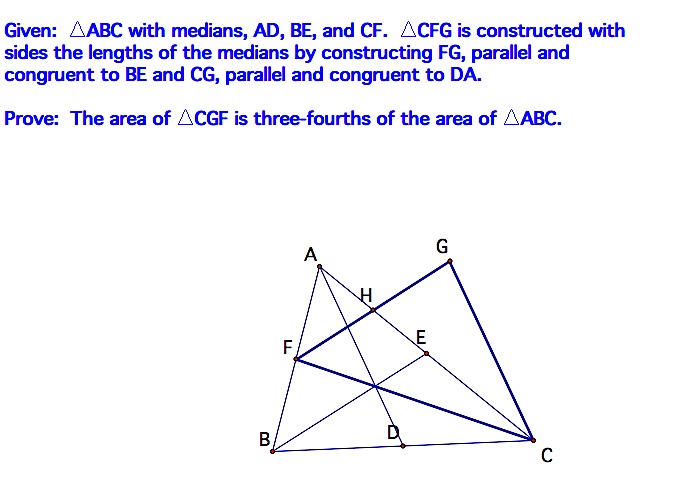