

Altitudes and Orthocenters
by
Jackie Ruff
We are going to examine several triangles, their orthocenters, and related triangles. First of all, an orthocenter of a triangle is the point of concurrency of the three altitudes.
So, if the triangle is acute, the orthocenter is in the interior of the triangle. If it is a right triangle, it is located on a vertex, since two sides of the triangle have become altitudes for the other two vertices. If the triangle is obtuse, the orthocenter is located in the exterior of the triangle. See the drawings below.
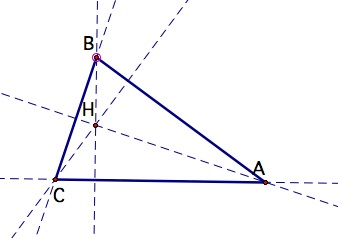 | 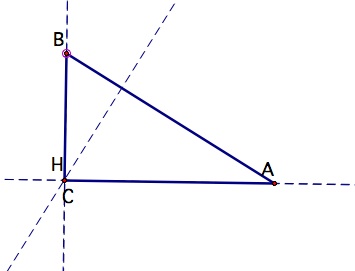 | 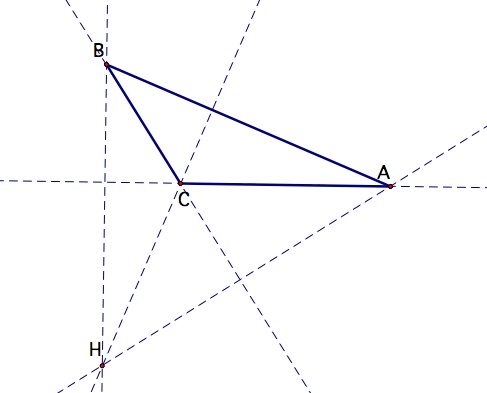 |
Next let's consider the triangles that we form by connecting the orthocenter in an acute triangle with the vertices of the triangle as shown below. We construct triangles ABH, ACH, and BCH. Look at the pictures below to see what happens when we construct the orthocenters of those three triangles.
 |  |
Point B is the orthocenter of triangle ACH and point A is the orthocenter of triangle BCH. Next we will add the circumcircles of the four triangles to our drawing.
 It appears that all four circles are congruent. Maybe we can prove that a little further along in this investigation.
It appears that all four circles are congruent. Maybe we can prove that a little further along in this investigation.
Next we will construct the nine point circle for each of the triangles - and when we do, we find that the nine point circles for each of the triangles is the same circle (see diagram below.)

In the diagram to the right, the red triangle is the nine point circle for each of the four triangles. We see that for triangle ABC, the nine point circle must go through the midpoints of the segments joining the vertices to the orthocenter. This requirement includes points E and F. It also must go through the foot of each altitude which includes point G (from vertex B). These three points determine a circle.
 Also,
point E is the midpoint of HA (the nine point circle goes through the
midpt. of the segments connecting the orthocenter with the vertices of
the triangle). So, NE is a midsegment for triangle HC(1)A making
it parallel to C(1)A and half the length of that side. Then we have proved that the radius of the nine point circle is half the radius of the circumcircle.
Also,
point E is the midpoint of HA (the nine point circle goes through the
midpt. of the segments connecting the orthocenter with the vertices of
the triangle). So, NE is a midsegment for triangle HC(1)A making
it parallel to C(1)A and half the length of that side. Then we have proved that the radius of the nine point circle is half the radius of the circumcircle. |  |
 | Let's start with a fresh picture of triangle ABC with orthocenter H. We have formed the three subtriangles by connecting the vertices with the point H. The nine-point circle has also been constructed. |
 | If we rotated triangle ABC 180 degrees using the center of the nine point circle as the center of rotation, the result is triangle A'B'C'. What is so interesting about this is in the next picture. |
 | Points A', B', and C' are the centers of the three circumcircles of our subtriangles. |
 | If we draw the segments from the orginal triangle's orthocenter (H) to the midpoints of the segments connecting point H to the vertices of triangle ABC, draw the corresponding segments for triangle A'B'C', and connect those midpoints for the two triangles, we have a two-dimensional diagram for a rectangular solid. |
 | By connecting the vertices of triangle ABC with those of triangle A'B'C', and drawing segments to H, we have a diagram of a large rectangular solid. |