We begin this investigation with a quick look at the parobola in the xy plane.
Recall the general form for the parobola is given by the equation
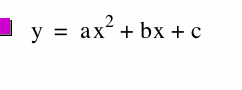
Which produce this graph

If we change the valye of a then we get verticl expansion if a >1 and refelection over the x axis if x<0
Here is a set of graphs to illustrate
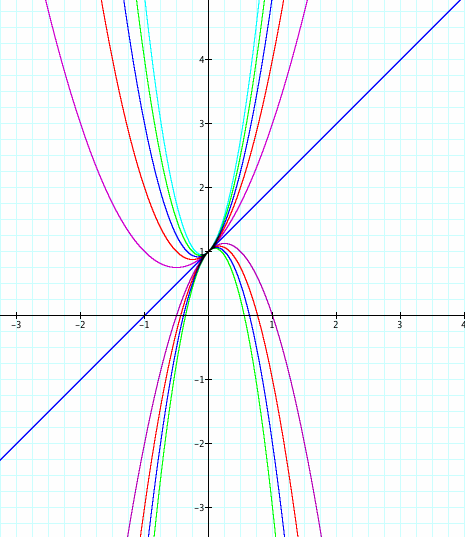
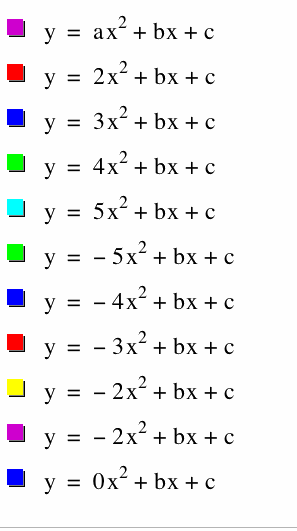
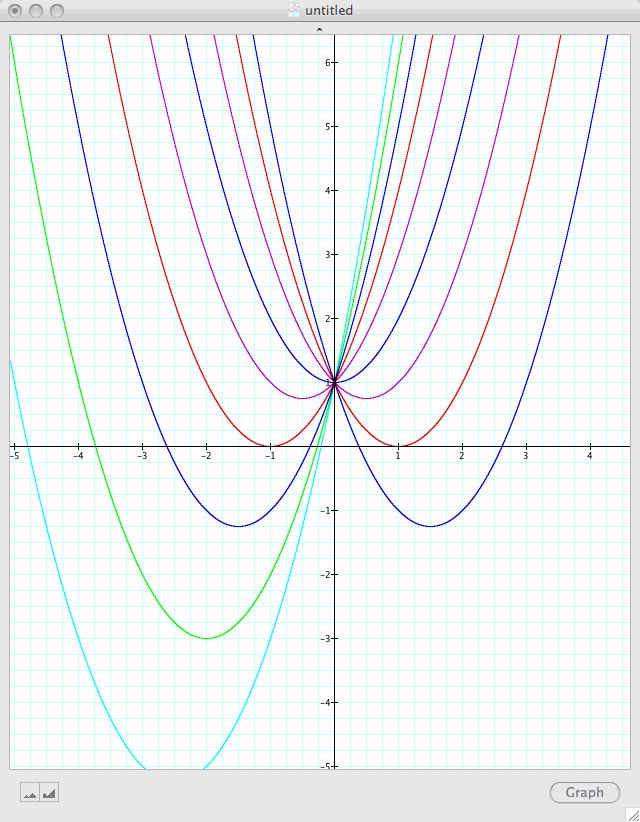
Also if we change the value of b we get the following set of graphs.
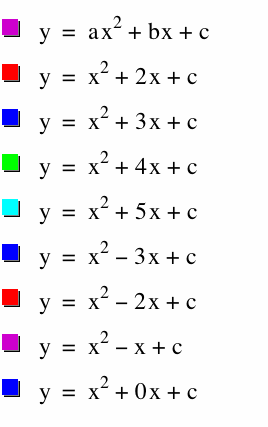
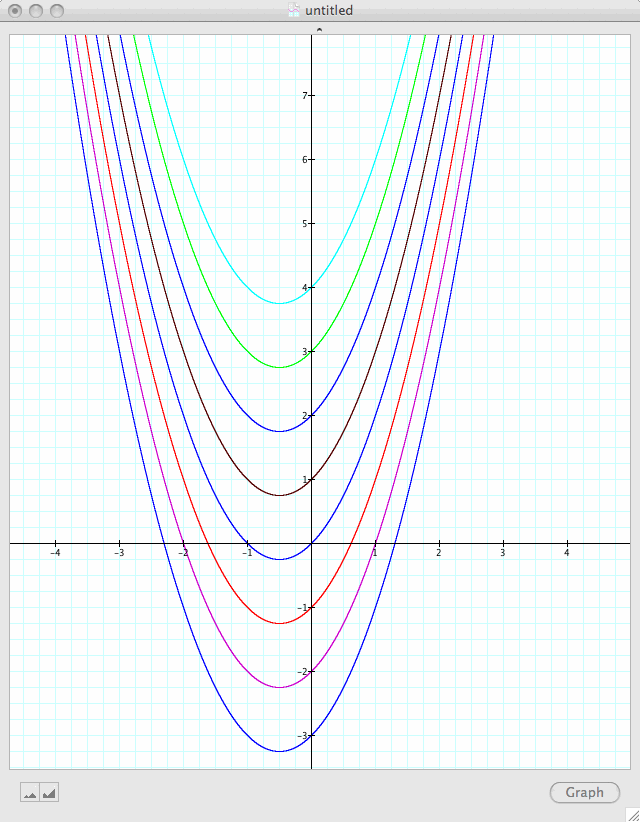
Now if we vary c the graph is a vertical translation. Take a look at this set of graphs
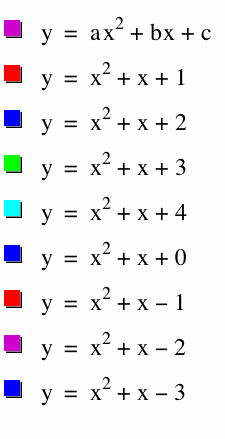
This type of exploration provides a visual, so that students can quickly graps the properties of the parobola without the complex algebra and memorization.
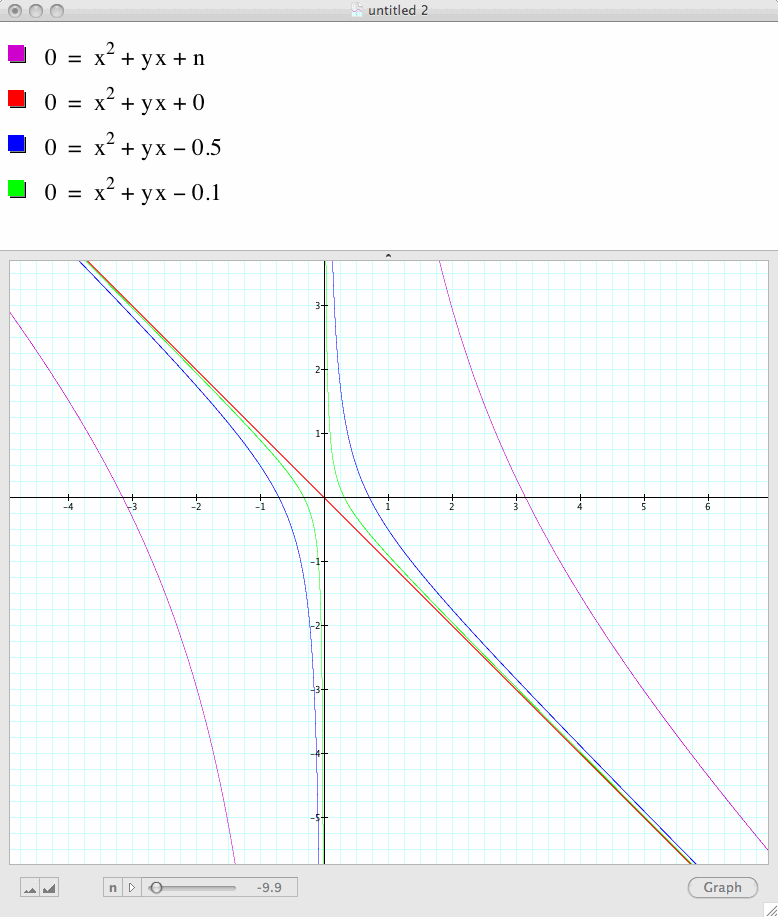
We proceed this investigation by looking at the xb plane
In order to graph the xb plane, we need to replace the b with y.
How the graph will look like this
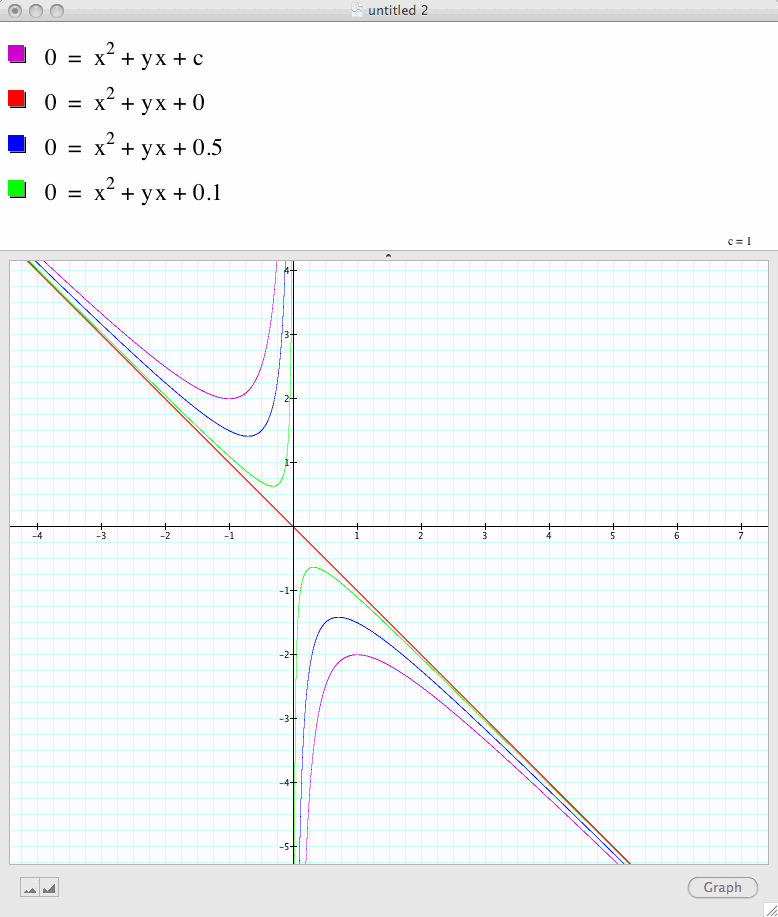
Note that for some value of b there is no real roots. In fact, from the graph we can conjecture that if c is large, the number of real roots decreases.
Also if c is negative we get this set of graphs, and we will always have real roots. Now compare this visual to the normal descrimant rule.