Investigation of The Pedal Triangle
by
Nathan Wisdom
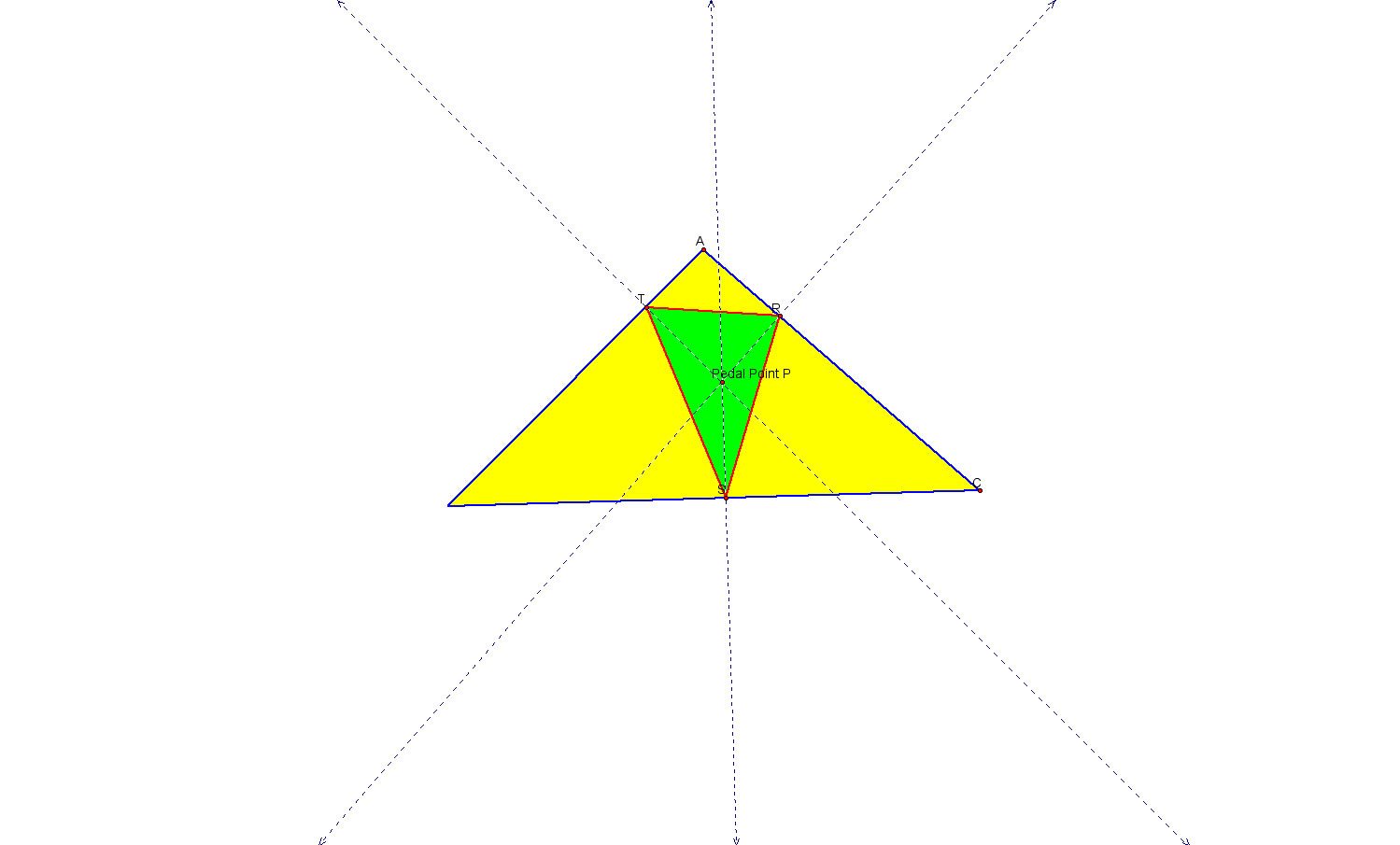
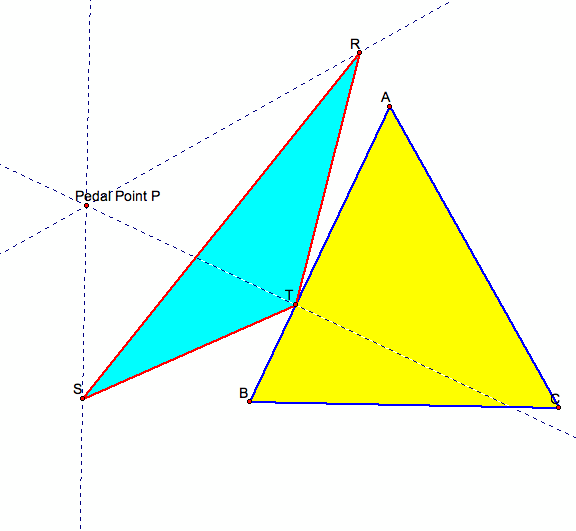
If we let triangle ABC be any triangle. Then if P is any point in the plane, the triangle formed by constructing perpendiculars to the sides of ABC to locate three points R, S, and T that are the intersections. The triangle RST is the Pedal Triangle for Pedal Point P. A GSP file with script tool is provided for you to explore. Here are two such pedal triangles. In the first one the pedal point is inside the triangle, and in the second the pedal point is outside the given triangle.
And...
The location of the chosen point P relative to the chosen triangle ABC gives rise to some special cases:
If if pedal point P is the centroid of triangle ABC we get..
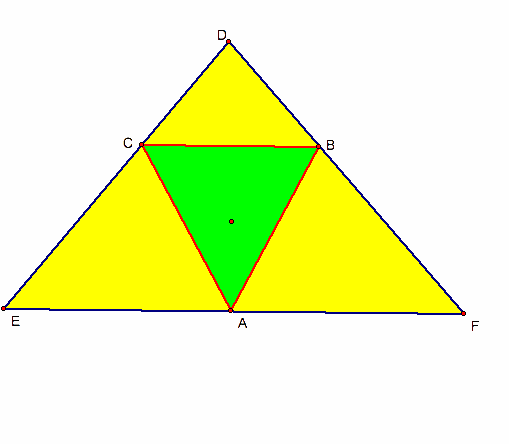
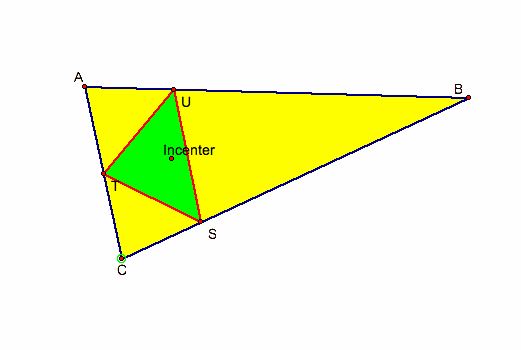
And if the pedal point P is the incenter we get the intouch triangle
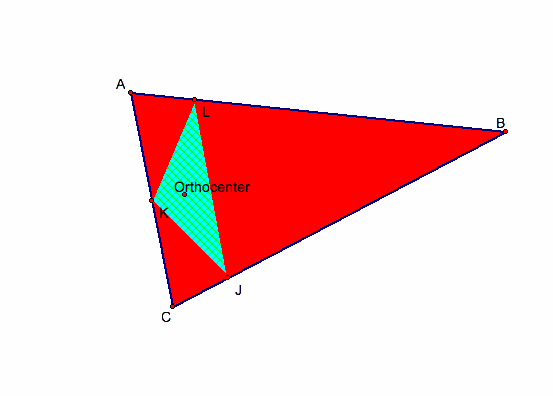
If P is the Orthocenter then we get the orthic triangle.
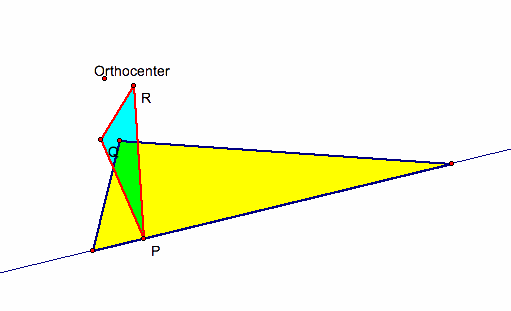
Even if outside ABC?
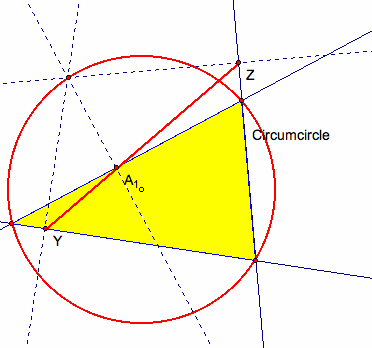
What if . . . P is the Circumcenter . . . ? Even if outside ABC?
If P is on the circumcircle of the triangle then we get the Simpson line.