
An Exploration of The Pythagorean Means
by
Nathan Wisdom

An Exploration of The Pythagorean Means
by
Nathan Wisdom
Historical Note
The relationship among the numbers 6, 8, 9, and 12 appeared to have
both acoustical and arithmetical peculiarity to The Pythagoreans. These
numbers were believed to be of special interest to The Pythagoreans.
For example, The number 9 is the arithmetic mean of 6 and 12, and the
number 8 is the harmonic mean of 6 and 12. That is:
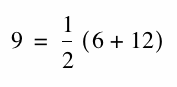
and
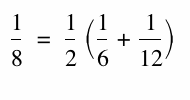
Further, 6 is to 8 as 9 is to 12, and 6 is to 9 as 8 is to
12, or
The arithmetic mean of two numbers was defined by The Pythagoreans as a
number such that the mean exceeds the first number by the same amount
as the second number exceeds the mean. Thus,
9 − 6 = 12 − 9
In other words the arithmetic mean of two numbers can be defined as one
half their sum. Thus, the arithmetic mean of 6 and 12 is
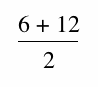
The geometric mean of two numbers was defined as a number such that the
difference of the geometric mean and the first number divided by the
difference of the second number and the geometric mean is equal to the
first number divided by the geometric mean.Thus, 6 is the geometric
mean of 2 and 18 because
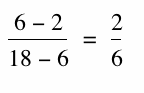
The modern definition is: The geometric mean of two numbers is the
square root of their product. Thus,
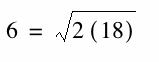
The harmonic mean of two numbers was defined as a number such that the
difference of the harmonic mean and the first number divided by the
difference of the second number and the harmonic mean is equal to the
first number divided by the second number. Thus, 8 is the harmonic mean
of 6 and 12 because
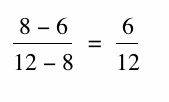
An Equivalent definition of the harmonic mean, H, of two numbers a, and b, is
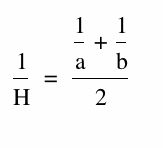
The High School Geometry Context
The High School Geometry introduces the geometric mean as either: (a) Right triangle relationship; (b) Application and proof of the Pythagorean Theorem; or (c) Similarity of right triangles.The
arithmetic mean is taught as and algorithm in data analysis and
probability. No connection is made to the geometric
interpretation of the arithmetic mean.The mid segment theorem for
trapezoids is a part of the high school geometry curriculum, but, very
few teachers help students to make the connection between the
arithmetic mean and the mid segment of a trapezoid. The harmonic mean is
not particularly mention in the mathematics curriculum, and is not part
of the new Georgia performance standards. Only a few mathematics teachers
knows about the quadratic mean.
High school Geometric mean.
When the geometric mean is discussed in high school, three main
theorems are presented to students. The theorems are as follows:
Theorem 1.
If the altitude is drawn from the vertex of the right angle of a
right triangle to its hypotenuse, then the two triangles formed are
similar to the given triangle and to each other.
Theorem 2.
The measure of the altitude drawn from the vertex of the right
angle of a right triangle, to its hypotenuse is the geometric mean
between the measures of the two segments of the hypotenuse.
Theorem 3.
If the altitude is drawn to the hypotenuse of a right triangle,
then the measure of a leg of the triangle is the geometric mean between
the measures of the hypotenuse and the segment of the hypotenuse
adjacent to that leg.
Construction and Exploration of The Means
We will now look for construction of the means using the theorems and
definition of the means. The Geometer sketchpad will be used to do the
constructions.We will denote the arithmetic mean as A, the geometric
mean as G, the harmonic mean as H, and the quadratic mean as Q. The
quadratic mean is also known as the root mean square.
|
Construction of means using a trapezoid of base a, and b. |
How were these means constructed? We will discuss the construction of these means but first let us look at another construction.
| Construction of the means using a semi circle with diameter a+b. | 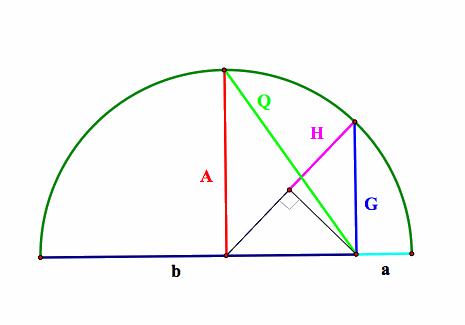 |
The construction using the semi circle is more appropriate for the high school classroom because the construction is much quicker. This is a good tool for demonstration and discussion. Students should be able to prove using algebra that these means are consistent with given segment a, and b.Discussion and Proofs.Let us first look at the construction bog the means using a trapezoid. To construct the arithmetic mean A, we will use Mid-Segment theorem of a a trapezoid.
The mid segment theorem for trapezoids: The segment connecting the midpoints of the sides of a trapezoid is parallel to the base and its length is one half the sum of the lengths of the bases.
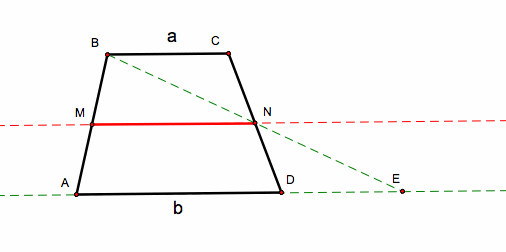 |
|
Therefore segment MN is the arithmetic mean A of a, and b.
We now look at the harmonic mean H of segment a, and b.
The segment parallel to the bases and passes through the intersection of the diagonals of the trapezoid is the harmonic mean H.
Proof:
|
|
We now look for a construction of the geometric mean G.


And finally we have this picture

Now the construction of the quadratic mean is a bit more involved then the other means. Let us first look for a segment that is equivalent to the quadratic mean. Consider the trapezoid ABCD.


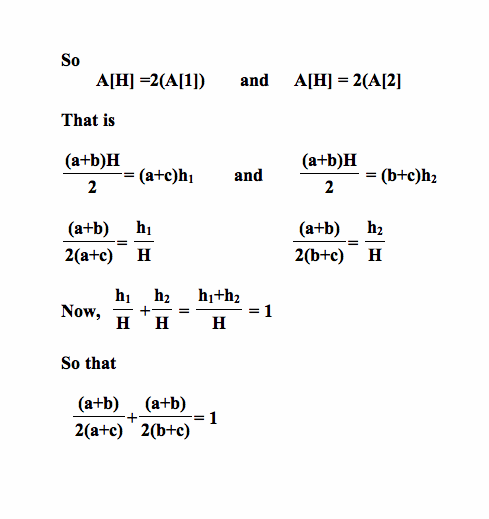
Now using basic algebra, we have
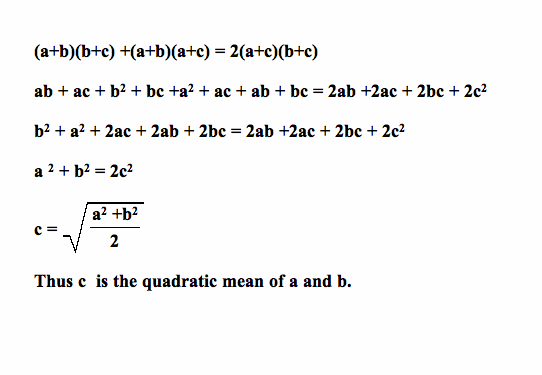
How do you construct such a segment?

Here is a picture of the construction:
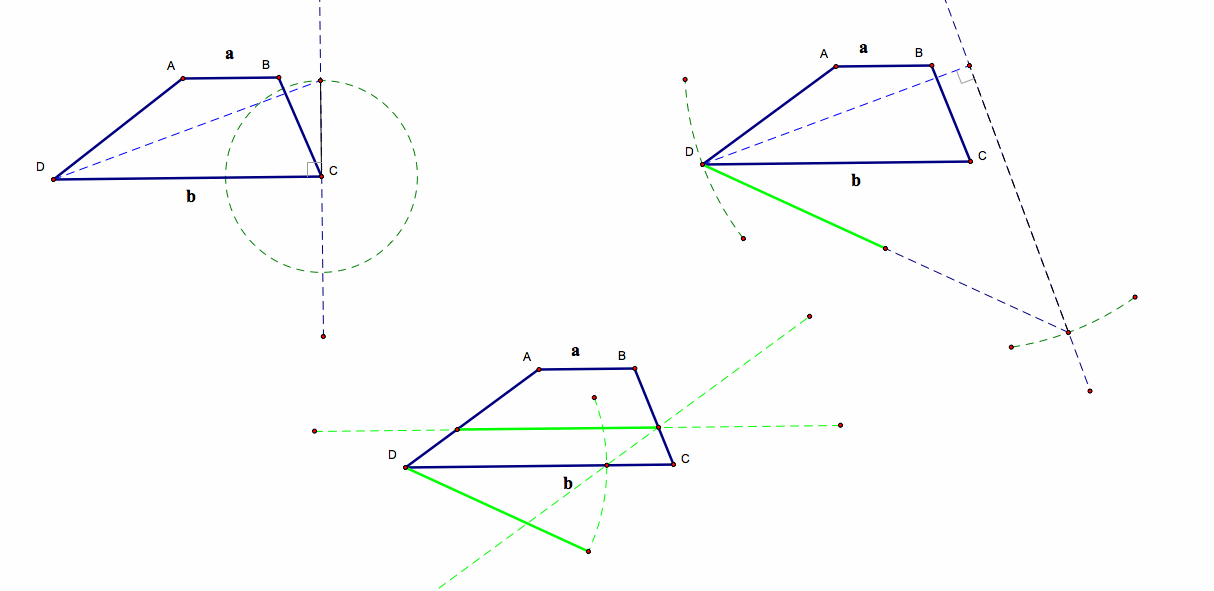
We will now look at the construction using the semi circle.
Given segment a, and b. 1. Construct segment of length (a + b) 2. Construct the mid-point M 3. Construct circle with diameter (a+b) 4. Construct perpendicular at B to meet the circle at D. BD is the geometric mean of a, and b. Why? 5. Construct perpendicular at M to meet the circle at E. ME is the arithmetic mean. Why? 6. Construct Segment BE. This segment is the quadratic mean |
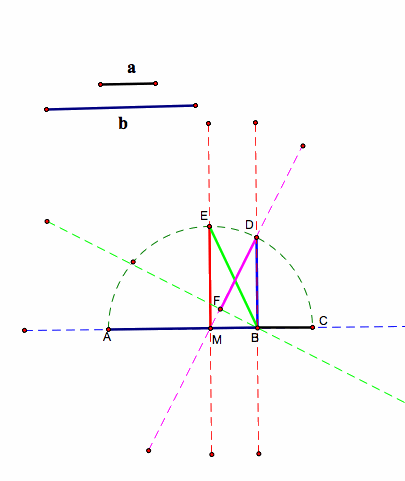 |
 |
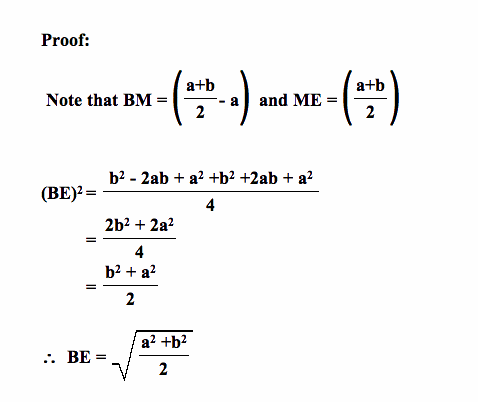 |
7. Construct perpendicular from B to segment MD to meet segment MD at F. FD is the Harmonic Mean.
 |
|
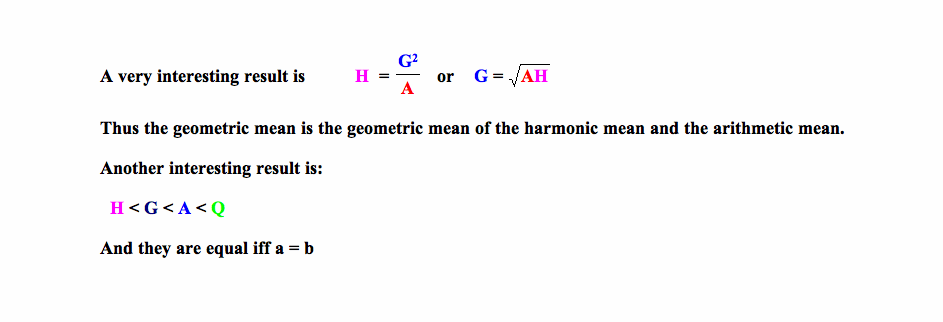
Reference