

Transformation Geometry and Symmetry for High School
by
Nathan Wisdom
The purpose of this project is to : (a) Develop a set of reference material that may be used by high school teachers to discuss transformational geometry and symmetry; and (b) To use technology to help students to visualize and solve problems involving transformation. There is a discussion of the use of matrices to build and use transformations which may help students to visualize animations used by the film industry for instance. This project does not include a problem set. The reader is however advised to to use GSP to explore the different transformations. Finally, GSP will provide useful conjectures, but will not provide a proof. Therefore, the proofs of properties and conjectures are left as an exercise,
Symmetry is the kind of pattern that a shape has. It deal with the exact matching of a position or form about a point, line or place. It is perhaps one of the most recognizable properties of figures.
(a) |
(b) |
(c) |
Figure 1
There are three types of symmetry that a plane figure can have:
(a) Translation Symmetry
(b) Reflection Symmetry
(c) Rotational Symmetry
A movement along a straight line without turning is called a translation. Thus a plane figure has translation symmetry if it can be translated and still look the same.
For example Figure 2
(a) |
(b) |
Figure 2.
A line of symmetry or the axis of symmetry of a plane figure is a line which can be used as a fold, so that one half of the shape covers the other half exactly. A plane figure can have one or more lines of symmetry. Example Figure 1
A Plane figure has rotational symmetry of a certain order if the plane figure maps on to itself under a rotation through some angle about the center. All plane figure has rotational symmetry of order 1. Since a rotation of 360 degrees about its center will map the figure back to itself. When discussing rotational symmetry, rotational symmetry of order one is not considered. Therefore a scalene triangle,( See Figure 3) does not posses rotational symmetry.
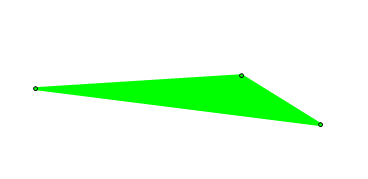
Figure 3
A Transformation describe the relation between any point( or object) and its image. A transformation is a one- to-one mapping of all points on the object onto corresponding points on the image. By one-to one we mean that given two distinct points A, and B in the plane, then under a transformation, the image of point A is different from the image of point B.
If P is a point on the plane and T is a transformation, then T(P) = P' and we say that T transforms P to P'.
For this project we will investigate the following hierarchy of transformations.
Identity |
Isometries |
Similarities |
Affine Transformations |
Topological Transformations |
There are six basic types of transformations:
The Identity is places the highest in the hierarchy of transformations, it requires that every thing be invariant by the transformation. Only translations and rotations are able to satisfy these conditions. Thus translation and rotation are both congruency transformations.
After identity is the isometries. These are the distance preserving, or length preserving transformations. Libeskind (2008), defined isometries as a transformation that preserve distance. Translation, reflection, and rotation are isometries, since they preserve length. Therefore translation, reflection and rotation are congruency transformations.
Now if we allow angles to be preserved although length is not, then we get to the dilation. Dilation, together with the isometries are similarity transformation
Further if we only require that parallel lines be mapped onto parallel lines, we get the shears and stretches. All the basic transformations mentioned are classified as affine transformations.
If only the order of points on an line, and the order of a node were important invariants, then we have topological transformations of networks.
Translations
A translation is a transformation of the plane in which a a plane figure slides along a straight line, and changes its position without turning. Each point moves the same distance and in the same direction. Hence all points subjected to the same translation undergo the same displacement. The transformation is completely defined by any one point. According to Libeskind (2008) The transformation of P to P' is such that if P is not on the line containing the transformation vector AB, then P' is the point in the plane for which ABP'P is a parallelogram, and if P is on AB then P' is the point for which ABP'P is a degenerate parallelogram. Recall that a vector quantity has both magnitude and direction, thus a translation vector has both magnitude and direction.
Properties of Transformations
When studying the different types of transformations, we try to discover the properties of the figure which remain unchanged after the transformation. GSP is a useful tool to explore.
 |
Thus any of the four displacement vectors describe the transformation.
|
Figure 4 |
We can conclude :
Translation in the coordinate plane
Column Vectors
A displacement vector or translation can be represented by a column vector or column matrix of the form:
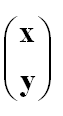
Thus if P is a point and P' is the image we say that if:
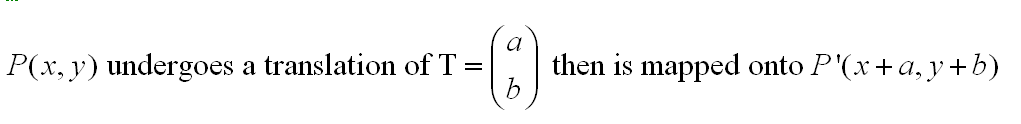
The definition can then be written as:
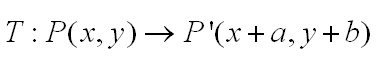
So
(Object Matrix) + (Translation Matrix) = (Image Matrix)
Using this coordinate or analytic approach is is easy to show that the composition of two translation is a single translation.
Here is an algebraic argument:
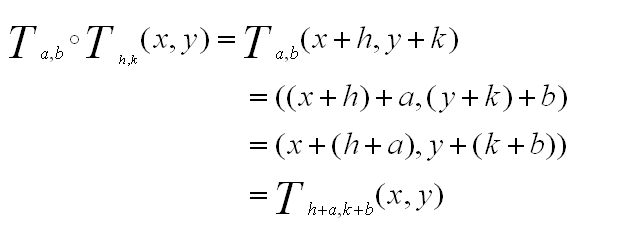
Using GSP we can also investigate the composition of two translations as in Figure 5.

Figure 5.
Reflections
A reflection in a line l is a correspondence that pairs each point in the plane and not on the line with point P' such that l is the perpendicular bisector of segment PP'. IF P is on l then P is paired with itself (Libeskind, 2008)
In the coordinate plane, reflection images over some lines are very easy to find. GSP is a very useful tool to demonstrate and investigate reflection over the x-axis, y-axis, line y = -x, and the line y = x.
Properties of Reflections
Here we investigate properties that are invariant under a reflection using GSP
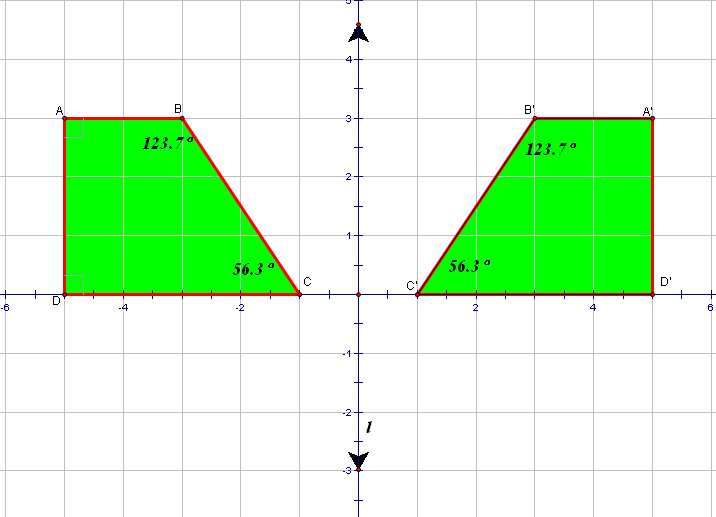
Figure 6.
We can conclude that:
Rotations
A rotation is a transformation in which every point turns through the same angle, about the same center, and in the same direction. In the plane, rotation is about a single point called the center of rotation. The center of rotation is the only point that does not change its position after rotation. A rotation can either be clockwise or counterclockwise. A negative angle means rotate clockwise and a positive angle means counterclockwise.
A formal definition from Libeskind (2008) : If O is any point and α is a real number, then the rotation about O through α, is a function from the plane to the plane that maps O onto itself and every point P on to P' such that OP = OP' and the measure of angle POP' = α.
Properties of Rotation
We will use GSP to investigate the properties of a figure which are invariant under a Rotation.

Figure 7.
After investigation with GSP we can conclude that:
Dilations
A dilation is a transformation which mops a shape onto a similar shape, from a center of dilation using a scale factor k. The scale factor is the ratio of the corresponding lengths of the image to those of the object.
We will use GSP to investigate four cases of the scale factor for dilations. Case1: k >1; Case 2: 0< k<1; Case 3: -1<k<0; and Case 4: k<-1.
Dilation with scale factor >1
|
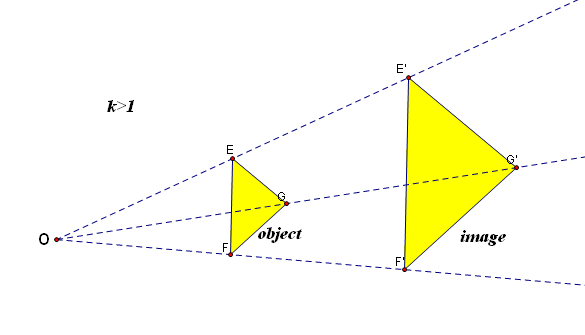 |
Dilation with scale factor < -1
|
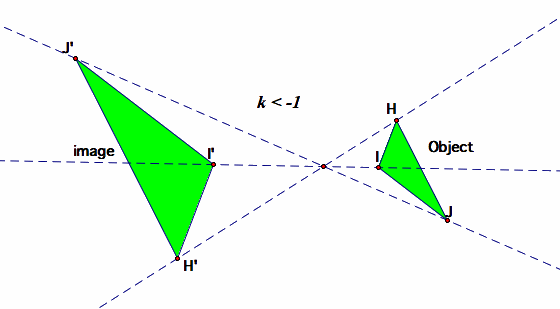 |
Dilation with scale factor between 0 and 1
|
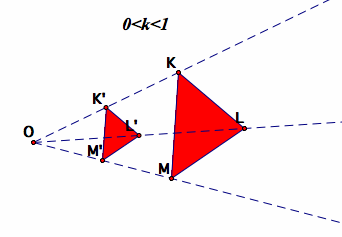 |
Dilation with scale factor between -1 and 0.
|
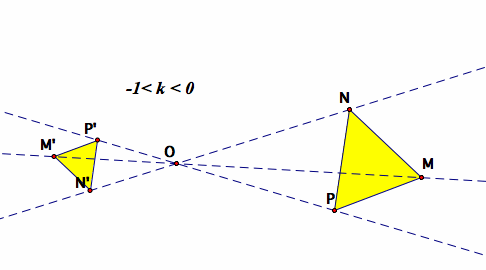 |
Figure 8.
Properties of Dilation
We will use GSP to investigate the properties of a figure that remain invariant under a dilation
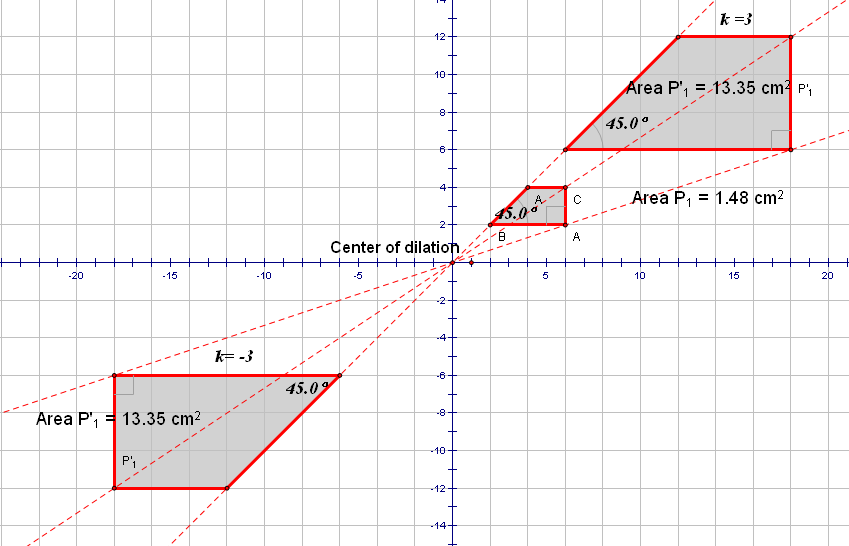
Figure 9.
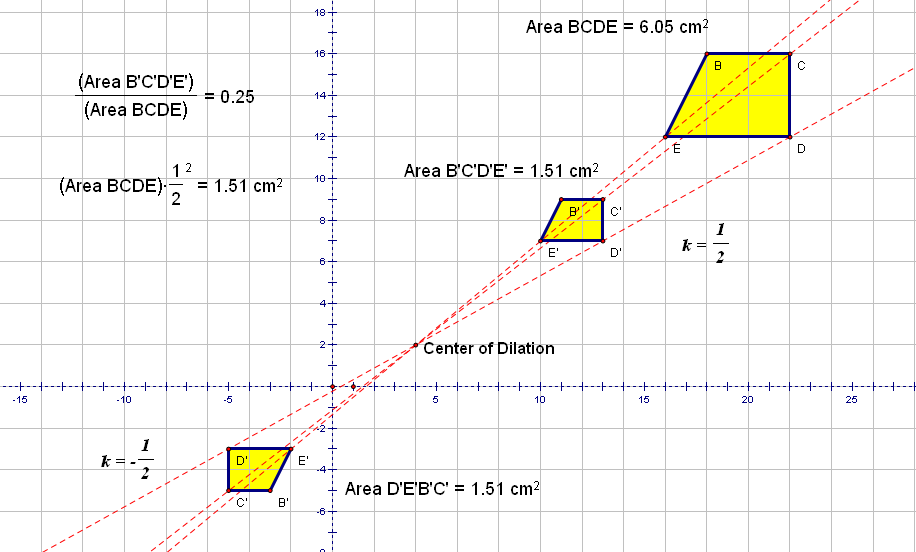
Figure 10.
Using GSP, as illustrated in Figure 8 to Figure 10. We can conclude that:
Shear
A transformation in which all points along a given line l remain fixed while other points are shifted parallel to l by a distance proportional to their perpendicular distance from l
We can use GSP to illustrate a shear. (Please note that GSP does not have a shear function)

Figure 11.
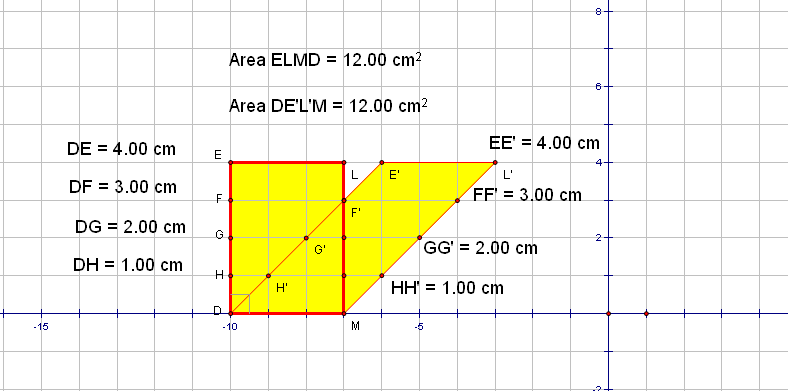
Figure 12.
We can conclude that a share is fully described if we know (a) the invariant line, and (b) the image of a point that is not on the invariant line. Thus
Stretch
A stretch is fully described if we know (a) the direction of the stretch, and (b) the ratio of corresponding lengths.
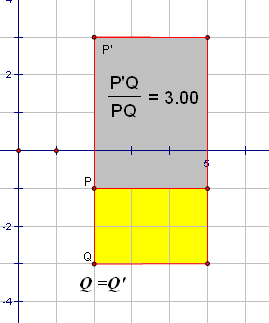
Figure 13.
Using the coordinate plane we can build and use transformation matrix for the different transformations.
As an investigation we can begin with the following questions:
How can a rotation with center at the origin be represented by a matrix?
How can rotation matrices be used to animate the rotation of two dimensional objects?
How can translation be represented using matrices?
How can dilation be represented using matrices?
How can we represent and transformation using matrices? Are there any transformation that cannot be represented using matrices?
How can we use matrix multiplication to investigate composition of transformations?
What limitations (if any) do you have when using matrix multiplication for composition of transformations? Is this limitation unique to any specific transformation?
How can we use composition of transformation to investigate complex animations?
In Search of New Isometries
Libeskind (2008) posed the question : Is there a unique isometry that maps any two points A, B to any other two points A', B'? We can use GSP to investigate this question even in high school geometry context. To restate The question we use the fact that an isometry is a congruence transformation. Then the question would be: Are there other congruence transformations?
Composition of three reflections
It is easy to see from the definition of reflection the the composition of two reflections in parallel lines m, and n is a translation of twice the distance between m and n. It is also easy to investigate that a the composition of two reflections in perpendicular lines is a rotation. However three reflections is not as simple. We will use GSP to look at three cases.
Case 1: three lines are parallel.
 |
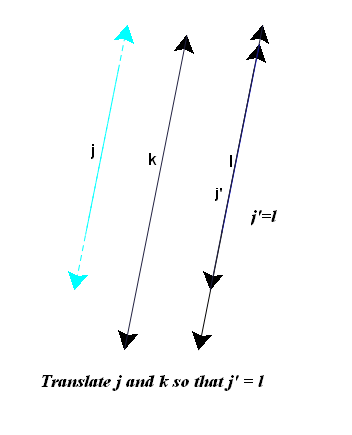 |
k' is not shown
Case 2: the three lines are concurrent
Case 3: a, b, intersect at P, ban c intersect at Q, Q ≠ P
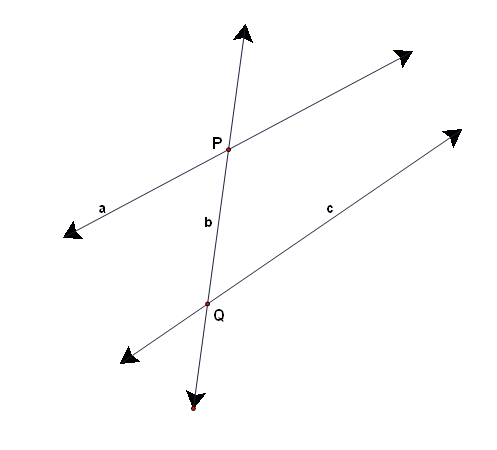 |
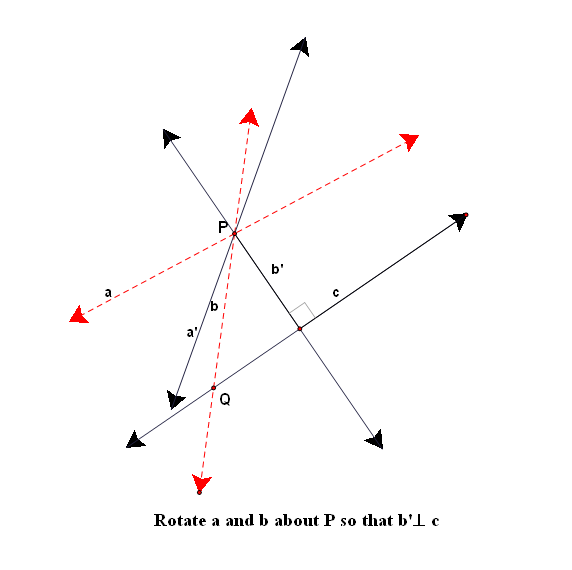 |
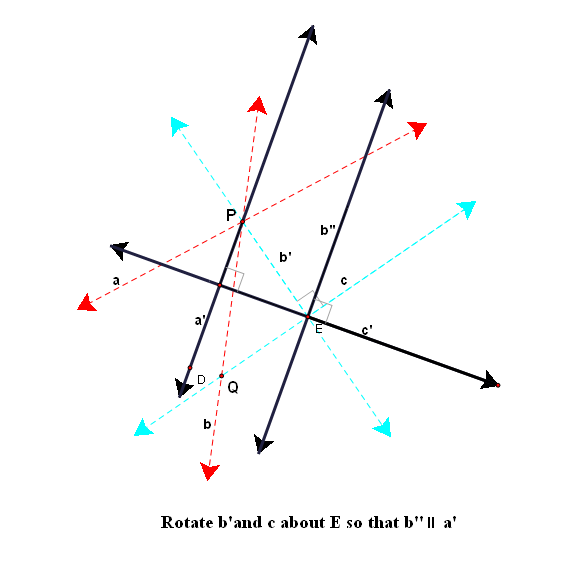 |
Thus we can conclude that the composition of three reflection is either a reflection or a glide reflection. This is essentially equivalent to Libeskind second fundamental theorem of isometries which states that every isometry is equal to a composition of at most three reflections.
Furthermore we can use GSP to investigate that every composition of reflections is either a reflection, rotation, a translation, or a glide reflection.
A further investigation is the discussion that with composition, the set of all congruence transformation is a group. This discussion is outside the scope of this project and is left to the reader to develop.
Reference
Libeskind (2008). Eucledian and Transformational Geometry: A deductive Inquiry. Jones & Bartlett, Sudbury, MA.
Weisstein, Eric W. "Affine Transformation." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AffineTransformation.html