

Quadratic Roots Made Easy
by
Priscilla Alexander
This write-up is for high school students who are being introduced to quadratic equations and their roots.
A quadratic equation is a polynomial of degree 2. When it is graphed it has the form of a parabola. For instance,
![]()
see graph
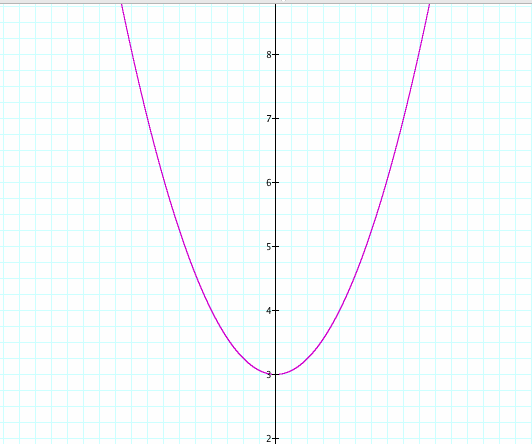
There are three ways to find the roots of a quadratic equation. The roots can be found numerically with a table. They can be solved symbolically with the quadratic formula. Lastly it can be solved graphically. See the animation for solving quadratic equations graphically.
The animation show the roots for the quadratic equation
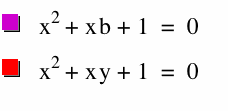
In the animation the y axis is equivalent to the b axis.
Where the red line intersects the parabola the x coordinate is the roots of the equation.
Let explore what happens when 2x+b =0 is added to the graph.
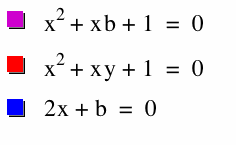
By looking at the first equation one can see that the third equation is the first derivative of the first equation. The first derivative of a equation gives and linear equation with the slope or rate of change and the y intercepts. From the animation it can be seen that the line created by the first derivative of the first equation intercepts where the equation has roots of the first equation. The relationship that this line has with the quadractic equation is when the solution has answer of plus or minus a number then a line can be created from that point.
It can be concluded from this exploration that the parabola has a linear equation that can be found that will intercept at one of its roots.