The Power of the Nine

by

Priscilla Alexander

 

This write-up is for the first year geometry student who is just being introduced to the nine point circle. We will explore how to construct the nine point circle and how to find its center.

A nine point circle can be constructed by finding the center of the nine point circle. To get the nine points follow the constuction below.

First construct a triangle and find the midpoints of the segments.

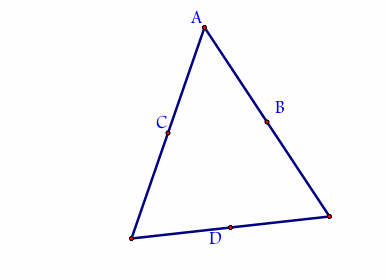
Next find perpendicular bisectors and label where they intersect with the sides of the triangle.

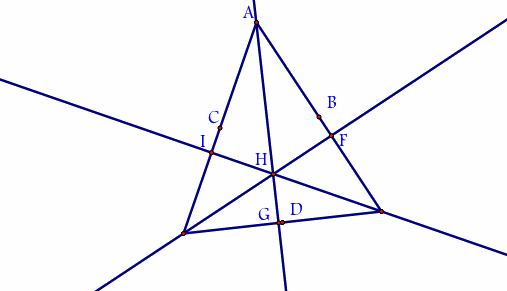
H is called the orthocenter because it is the point where all of the altitudes intersect.

Now find the midpoint of the segment from H to each of the vertices of the triangle.

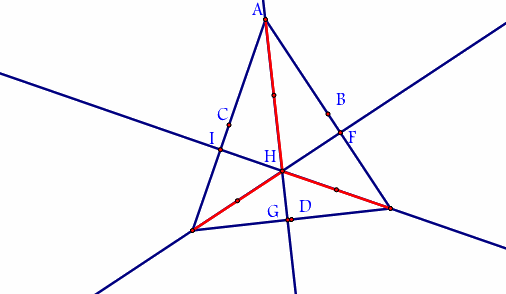
Here we have the nine points to connect are circle, but first we need to find the center of the triangle to find the circle that will connect all nine points together. We will do this by using a proof then we will construct it.

Proof:

First,when points C, B, J, and M are connected they form a rectangle. This is true based on the mid-segment theorem, which states that a midsegment connecting two sides of a triangle is parallel to the third side and is half as long. CB is the midsegment of triangle AKL, therefore its length is half of side KL and JM is the midsegment of triangle HKL, therefore its length is half of side KL. Therefore segments CB and JM are equal. Then, again by the mid-segment theorem, MB equals JC because each is one-half the length of AH. So connecting these points form a rectangle.

By definition a rectangle is a special kind of parallelogram. Second, the diagonals of a parallelogram are congruent and bisects each other.Therefore, point P is the midpoint of segments JB and CM. From this point it can be concluded that points C, I,J,G,D,M,F,B, and N are equal distance from point P. This is the definition of a circle.

 

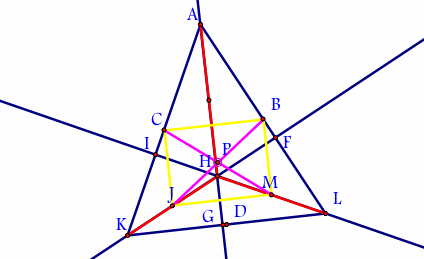
From point P a circle can be created to construct the circle that contains the nine points.

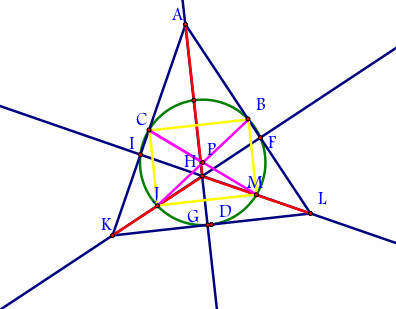
In conclusion, it can be seen that the nine point circle can be construted by finding the nine points and using the midsegment theorem to find segments that form a rectangle. Then the properties of the diagonals of a parallelogram can be used to find the center of the nine point circle.

return