

By
Priscilla Alexander
What Does the Tangent Circle Do!
This write-up is for students learning about tangent circles.
How to create a circle tangent to two circles in GSP.
First create two circles one inside of the other one. Next choose a arbitrary point on the rim of the larger cirle, and then draw a line through the center of the larger circle.
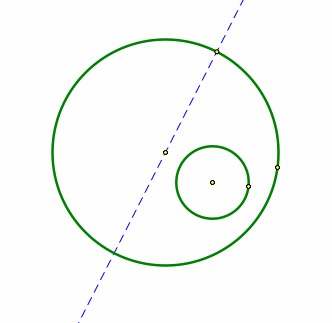
Then make a line segment of the radius of the smaller circle and then choose the arbitrary point and construct a circle by radius. Now choose the point of the new circle that intercepts with the line outside of the larger circle.
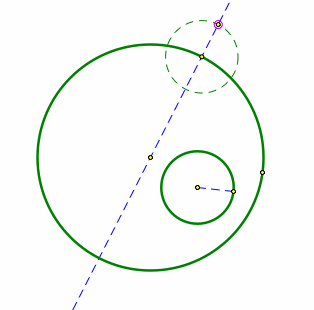
Connect the point on the dashed circle with the center of the smaller circle. Then take the midpoint of the line. Next, construct a perpendicular bisector through the midpoint.
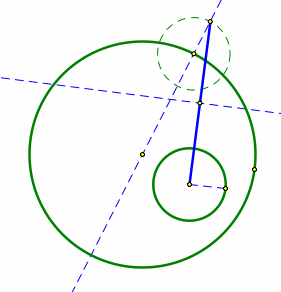
Where the perpendicular line and the line through the center of the larger circle intersects is the center of the tangent circle. Mark this point.
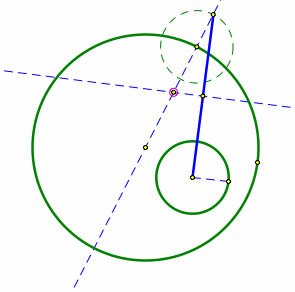
Select the midpoint and the point of intersection of the dashed circle and the large circle. Now construct a circle. This is the circle that is tangent to both circles.
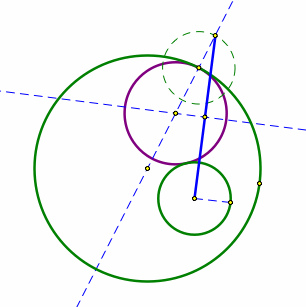
Animate the arbitrary point. See GSP sketch.
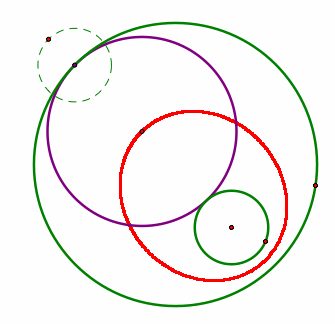
The purple circle is the created tangent circle and the red circle is the ellipsed formed when the tangent circle is animated. From this it can be concluded that the circle tangent to both of the circles, when traced, forms an ellipse.
Now that we know how to construct tangent circles, the question can be asked ,what type of shape is formed by the tangent circle when the two circles intersect ?
When the tangent circle is formed from two circles that intersect, when animated, an ellipse is formed and the foci are at the center of the two intersected circles.
What shape does the tangent circle make with disjoint circles.
Case 1: When one circle is larger than the other and arbitrary point is on the larger circle
Case 2: When one circle is larger than the other and the arbitrary point is on the smaller circle.
Case 3: When both circles are the same size and the arbitrary point is on either circle.
For case 1 the tangent circle forms a hyperbola that is equal distance from the two disjointed circles.
For case 2 through investigation it can be found that a circle that is tangent to both circles cannot be created. However, the circle created becomes tangent to both of the circles independently. In addition, the tangent circle becomes tangent to the vertices of the hyperbola that is formed by the animated path.
When both circles are the same size the tangent circle forms a hyperbola that is equal distance from both circles. See sketch