

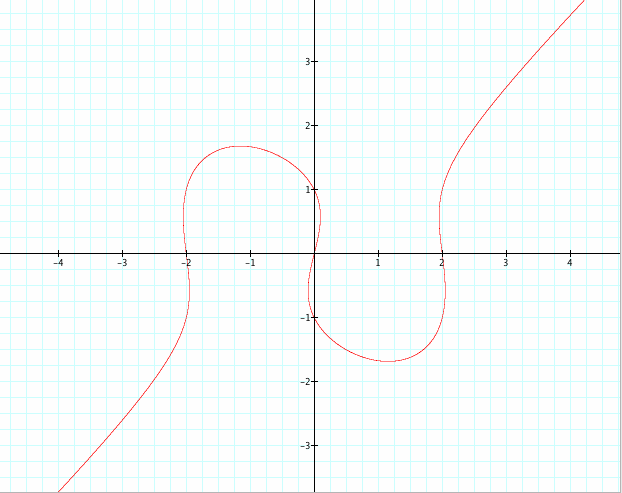
In this assignment I am going to give you some examples for some forms of exponential equation x( x² - 4 ) = y(y² - 1 ).
1) Examining the graph of x( x² - 4 ) = y(y² - 1 ) equation for different values of constant 4 from left side of the equation:
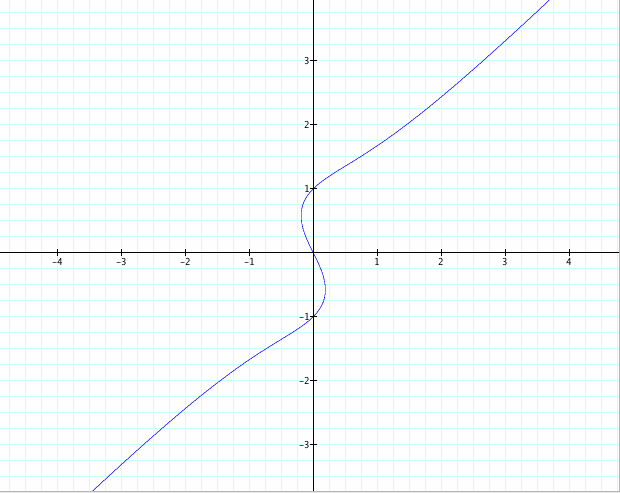
Here is the graph of x( x² - 4 ) = y(y² - 1 ):
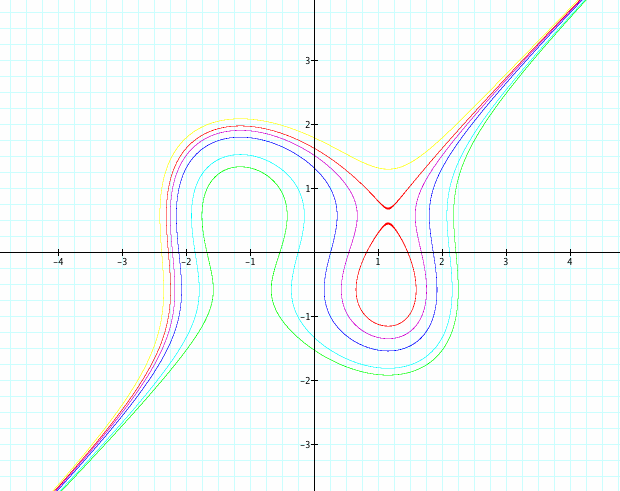
Now what happens if the 4 is replaced by other numbers? If we change the value of 4, we can see the changes on the graph, . The graph below shows a set of curves that resulted when 4 is replaced by (5, 2, 1,0.9, 0, and-2):
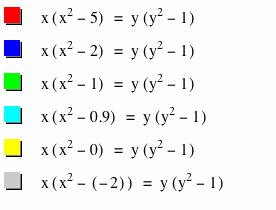
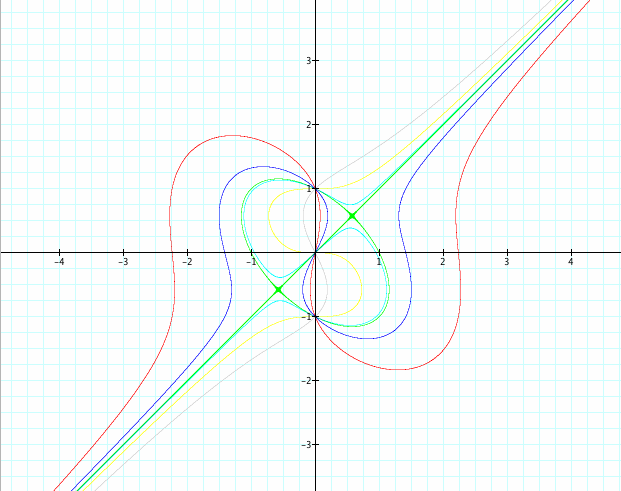
It appears that as the number replaced with smaller numbers, the curve of the equation gets smaller and starts to form an oval shape as an elliptical form.
The interesting thing about them all is that they intersect in three places (0,1), (0,-1), and the origin (0,0).
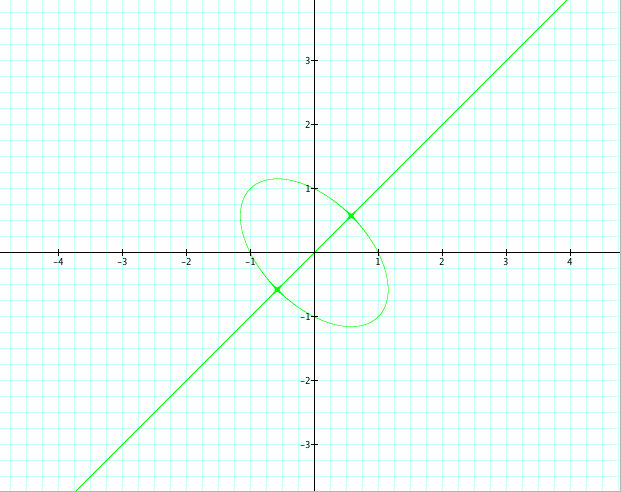
Note: The case when 4 is replaced with 1 then we get the above graph.
When 4 replaced with 1, that graph creates a straight line through (0,0) and it’s the only one that does that. It appears as if this graph is an intersection of the line y= x and an ellipse of some form.
Note that if we add -2 to the left hand of the equation we get the following graph for the equation. When 4 is replaced with a negative number, the elliptical form becomes narrower and is vertical, not sideways.
What happens if a constant is added to one side of the equation? The following set of graphs shows what happens when the constant {4,e,2,1,-1,-2} is added to one side of the equation.
![]()
Here is the graph of x( x² - 4 ) + e = y(y² - 1 ), e = 2.71828183
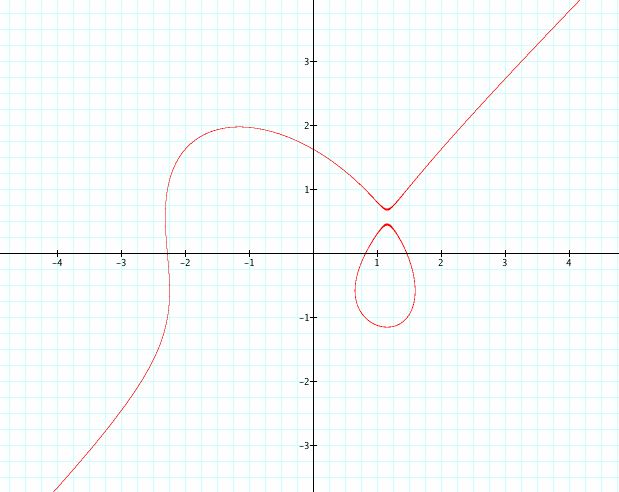
Now consider graph of x( x² - 4 ) = y(y² - 2 ). This graph is shown below:
Consider if we give value larger than 2 or smaller than 1:
2) Now lets check the graph of x( x² - 4 )-y(y² - 1 )=z equation: