

Assume we are given a square such that ABCD with segments AH, AG, BE, BH, CF, CE, DG, and DF which trisect the angles A, B, C, D. Now, we need to prove that
1) EFGH and IJKL are squares.
2)Area(EFGH) = 3Area(IJKL)
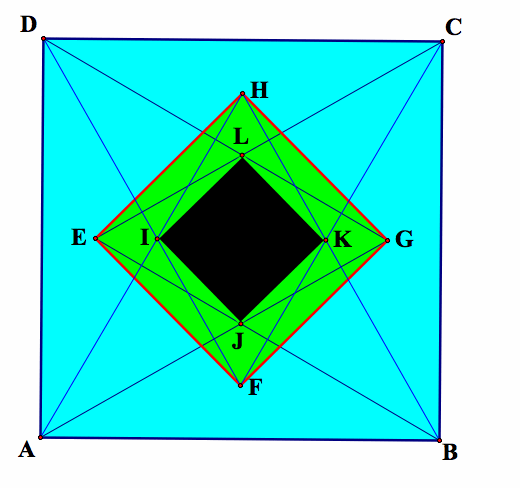
The link for this problem is:
http://gogeometry.blogspot.com/2009/11/problem-396-square-angle-trisectors.html
GSP document to draw above squares.
1) To show EFGH and IJKL are squares, I used GSP. As you can see below picture, first I draw midpoints of sides AB, BC, CD, and DA then when I connected opposite midpoints H,L,J, and F lies on the segment MN and E,I,K, and G lies on the segment OP. Thus all vertices lie on whether the segment MN or OP. Since ABCD is a square MN and OP are perpendicular to the sides of ABCD. Also we know the segments AH, AG, BE, BH, CF, CE, DG, and DF trisect the angles A,B,C, and D. Since MN is perpendicular to OP then they make a 90 degree angle in their intersection. Therefore, the distances from that intersection point to the vertices of EFGH and IJKL are the same. This means the vertices of these two quadrilaterals have angles 90 degree. Thus, EFGH and IJKL are squares.
We can also see this solution from below picture. Since the vertices H,L,J, F and E,I,K,G lie on the perpendicular segments MN and OP, EFGH and IJKL are congruent to the ABCD square therefore these two are squares.
A GSP picture to understand above explanations.
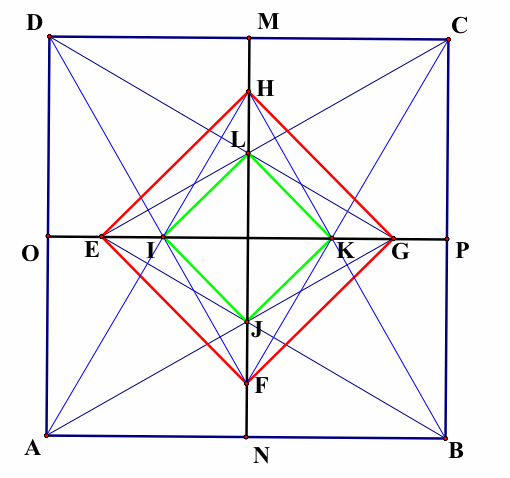
2) Now, assume we call the length of AB = a. MF is the perpendicular bisector of DFC triangle, then MF = (a/2).√3 = HN ( by the same argument).
MF+HN = a+HF this means
(a/2).√3+(a/2).√3 = a+ HF
HF= a√3-a
We know the area of a square = 1/2 multiply of perpendicular diagonals, this mean AREA(EFGH) = 1/2. HF.EG and HF= EG = a√3-a
So the AREA(EFGH) = (1/2) ( a√3-a ) a√3-a ) = 2a² - a²√3
Now by the same approach LM = JN = a/2√3 = a√3/6 and LJ = MN- (LM+JN) then LJ = a - 2(a/(2√3)) = a - a/√3
So the AREA(IJKL) = 1/2 . (a - a/√3) (a - a/√3) = 1/2.(4a²/3 - 2a²/√3) = 2a²/3 - a²/√3 = 2a²/3 - a²√3 / 3 = 1/3. ( 2a² - a²√3)
= 1/3.AREA(EFGH) or another mean
AREA(EFGH) = 3.AREA(IJKL)