Polar
Equations
ÒN-Leaf
RoseÓ
by
Tonya
DeGeorge
In this investigation, we will be looking at two different functions:
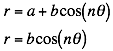
where a and b are equal and n is an
integer
LetÕs begin by looking at the first function. LetÕs begin with a simple case, where a and b are equal to one and n is zero. The following is a graph that represents this function:
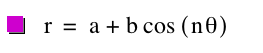
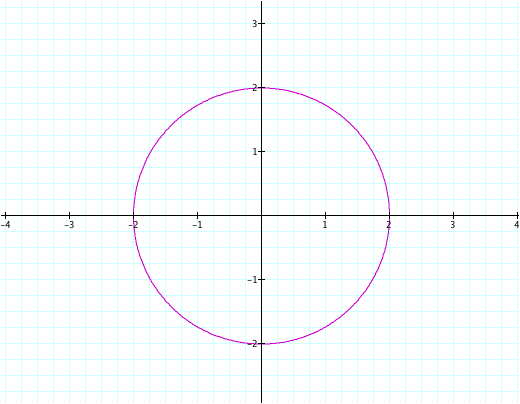
As we can see, when n is equal to zero, we get cos(0) which is equal to one. Hence we get a circle, where the radius is equal to two. Now letÕs take a look at nontrivial cases.
Suppose n is negative. What kind of picture do we get? LetÕs begin with n = -10 (with a and b still equal to one):
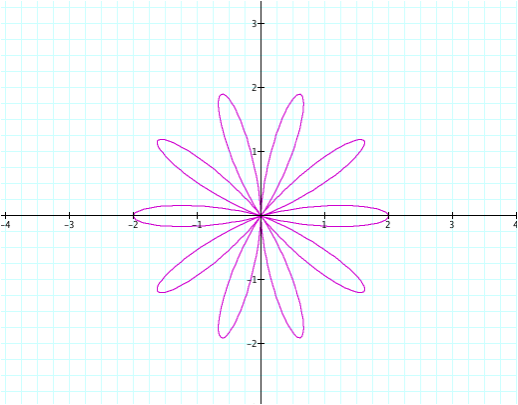
What do you notice about this graph? It looks like the circle has turned into a ÒflowerÓ with ten Òpetals.Ó Does this have anything to do with the value of n? Now letÕs try n = -8 to see if we get eight ÒpetalsÓ in the next graph.
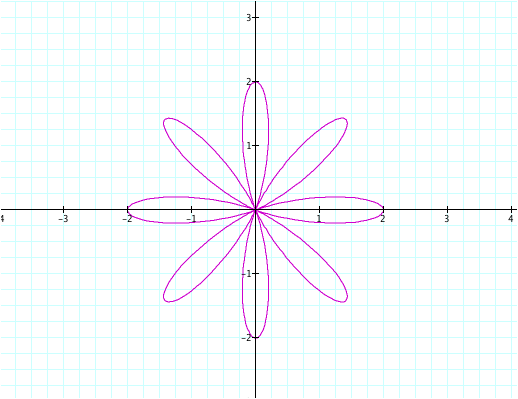
Again, it appears that the value of n determines the number of ÒpetalsÓ in the graph. Observe the graphs below (with corresponding n values).
n = -6 n = -4
n = -2
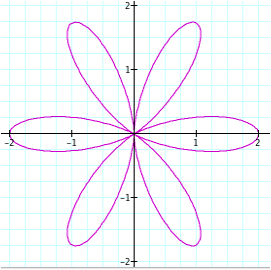
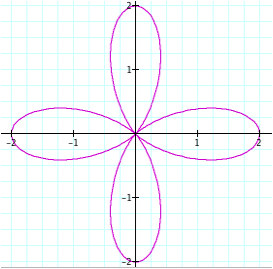
Now, this is interesting. Would we get the same type of graphs if we had used positive values of n? LetÕs investigate this further. Observe the graphs below:
n = 2
n = 4
n = 6
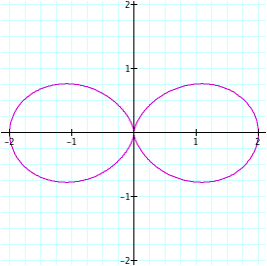
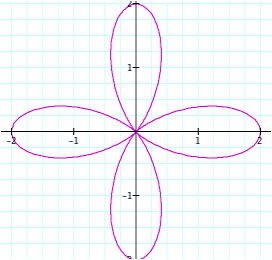
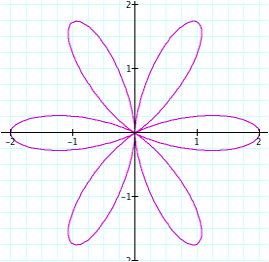
So it appears that the |n| determines the number of ÒpetalsÓ on the graph. The sign of n does not affect the graph (as long as n is even).
Did you notice that we chose all even values of n? Would this have changed if we chose an odd value? LetÕs graph some odd values of n:
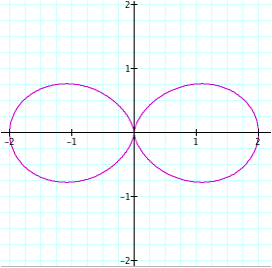
n = 1
n = 3
n = 5
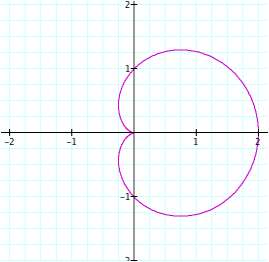
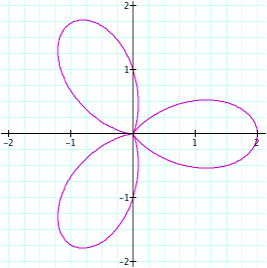
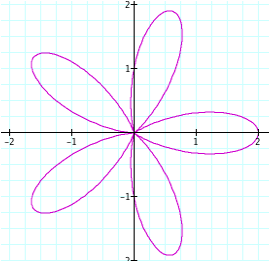
Now the problem becomes more interesting. It seems like at the value of n = 1, the graph is beginning to take on the shape of a flower (right now it resembles a lima bean). So essentially, this graph does have one Òpetal.Ó Likewise, the other graphs are still showing n number of ÒpetalsÓ (when n is three, there are three petals, etc.). However, although the other graphs look similar to the ones we saw earlier (for even values of n), there is something different about them. It looks as though the graph was rotated. In order to check if this is true, we will have to look at the graph in motion.
Now what if we change the values of a and b? We know only that a and b are equal, but what affect do these parameters have on the graph of the function? LetÕs try different values of a and b (and when n = 4):
a = b = 3
a = b = 2
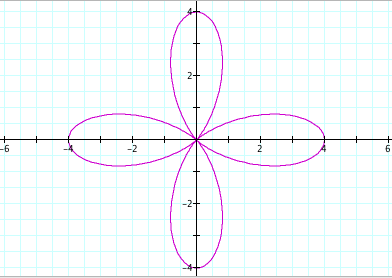
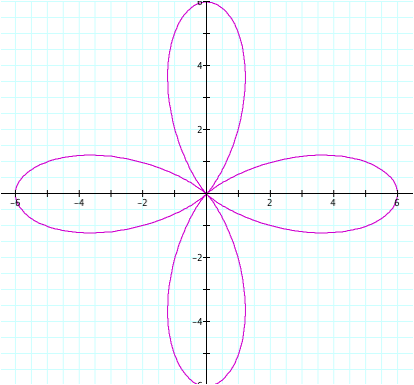
Conclusions:
¯ The number of ÒpetalsÓ of
the graph is determined by |n|
¯ If n is odd, the graph is rotated slightly to the right
¯ If n is zero, the graph is a circle with a radius equal to (a + b)
¯ The movement of the function
as n goes from -10 to 10 shows the
function starting at an initial value of 2 (when a and b were equal to
one) and creating the ÒpetalsÓ of the function
¯ a
and b changes the size of the graph
What if we took out the a term? How will the graph change? LetÕs look at the other equation posted at the beginning of this page:
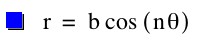
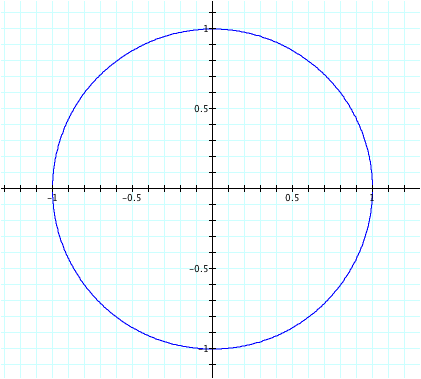
LetÕs keep b = 1 and look at how the graph changes as we vary n first. Again, letÕs begin with even values of n:
n = -2 n = -4
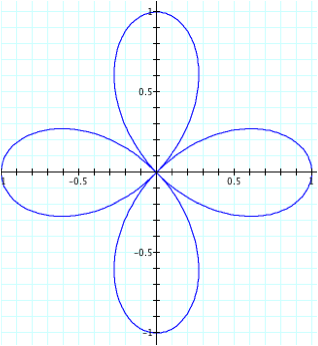
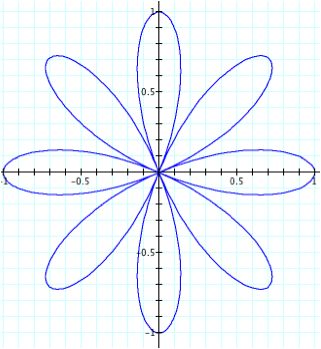
n = 2
n = 4
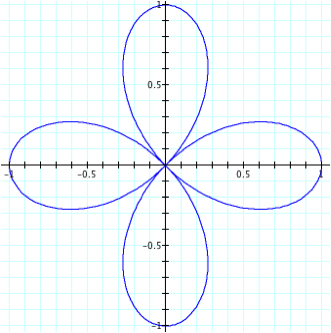
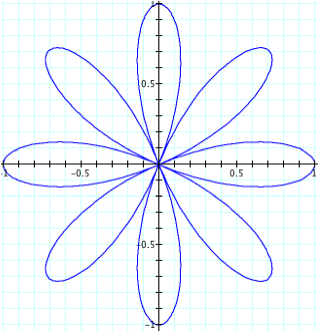
So although we get the same graph regardless of the sign of n, the number of ÒpetalsÓ is not dependent upon |n|. From the previous example, we would expect to get two ÒpetalsÓ but instead we get four. Likewise, we get eight ÒpetalsÓ when n is four. Hence, we can see that the number of ÒpetalsÓ in this case is dependent on |2n| or 2|n|.
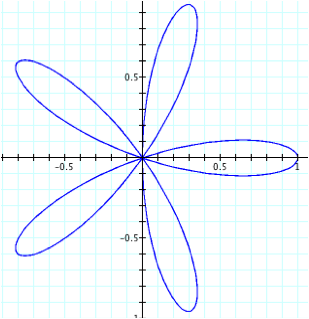
For odd values of n:
n = 3 n = 1
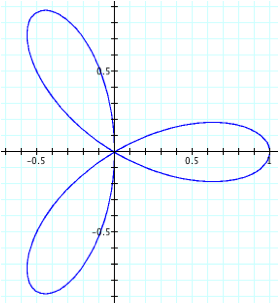
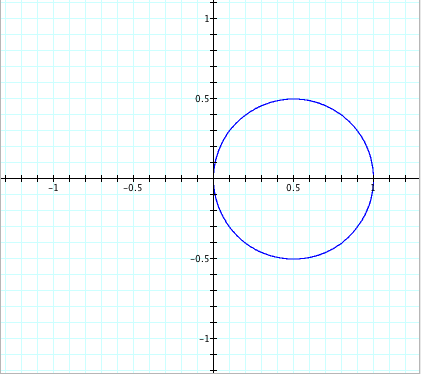
Take note that when n = 1, it does not look like a Òlima beanÓ as the first function did. Instead it is a circle with a radius of ½ with itÕs center at the point (1/2, 0).
n = 5
n = 7
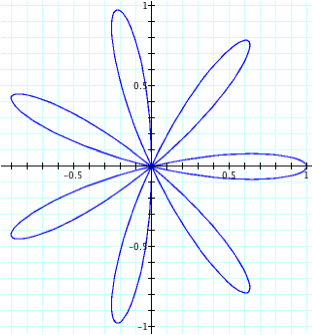
Now it appears that we get the same type of rotation, but again, it would be better to view this in motion:
It is important to notice that the petals seem to rotate more with this graph than the first one we looked at.
Finally, letÕs take a look at how the value of b affects the graph (for when n = 4).
b = 3
b = 3
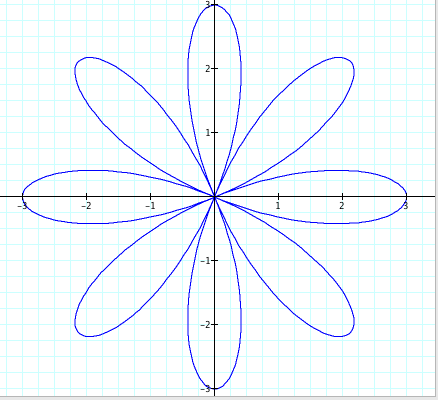
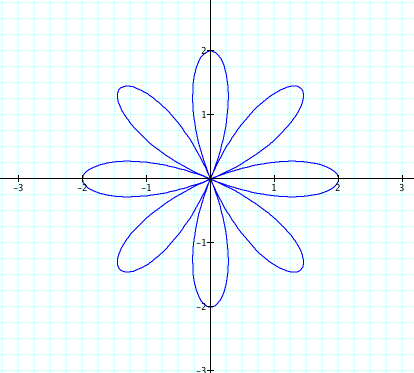
Conclusions:
¯ The number of ÒpetalsÓ of
the graph is determined by |2n| or 2|n|
¯ If n is odd, the graph is rotated slightly to the right
¯ If n is zero, the graph is a circle with a radius b
¯ The movement of the function
as n goes from -10 to 10 shows the
function starting at an initial value of 1 (when b is equal to one) and creating the ÒpetalsÓ of the function
¯ b
changes the size of the graph