---

Tangent Circles

By

Tonya DeGeorge

---

Here, we want to investigate tangent circles. The problem states:

Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point.

There are three possible cases to consider.

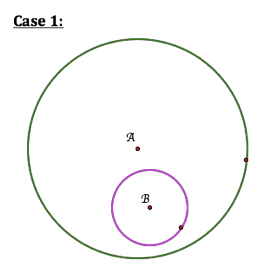
Ø Case 1: When one circle is inside another

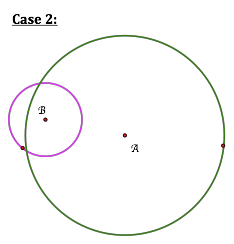
Ø Case 2: When the two circles intersect one another

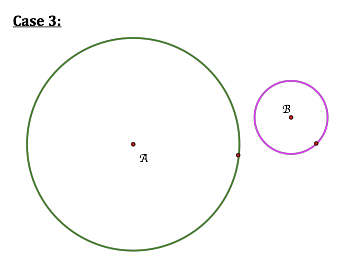
Ø Case 3: When the two circles are disjoint

Examples of each case are shown below:

Let’s begin with Case 1:

By using the tangent circle script tool created in Geometer’s Sketchpad, we can see the tangent circle (in red) constructed for Case 1:

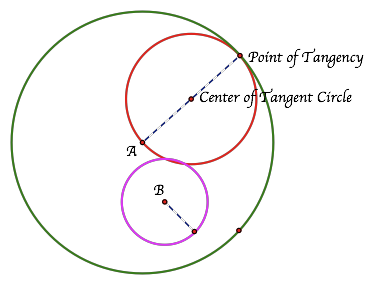
If we highlight the center of the tangent circle and then animate the point of tangency, we get an image (in yellow) which appears to be an ellipse.

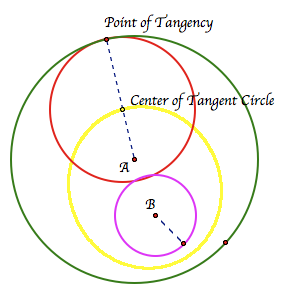
Let’s investigate Case 2:

Again, using the tangent circle script tool in Geometer’s Sketchpad, we get the tangent circle (shown in red) and the locus of points (shown in yellow). Again, it appears that the locus of points of the center of the tangent circle is an ellipse.

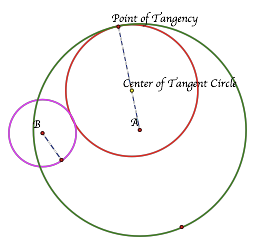
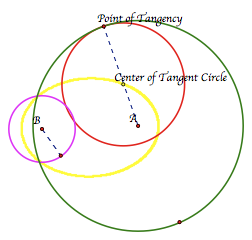
Let’s investigate Case 3:

From here we can see that the tangent circle (in red) is actually encloses circle A. From this observation, we should expect something different to occur.

By animating the point of tangency and by highlighting the locus of points of the center of the tangent circle, we see that a hyperbola is formed.

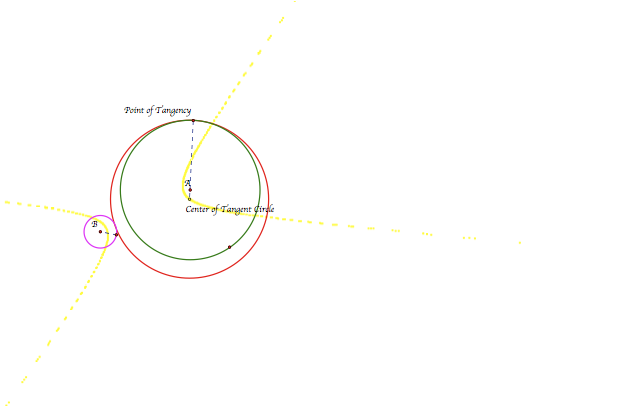
From this observation, we have found that the locus of points of the center of the tangent circle will form an ellipse as long as the two original circles intersect or one is inside the other. If the two original circles are disjoint, then the locus of points of the center of the tangent circle will form a hyperbola.

---

Return

---