Grazing Area

by

Megan Dickerson

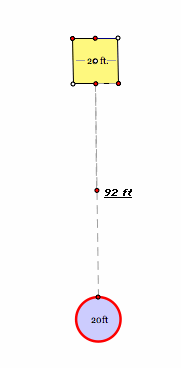
This problem asks for me to explore the area over which a goat can graze if a stake is moved along a line segment from the midpoint of the side of a shed to the edge of a silo. The rope to which the cow is tethered measures 76.7 ft. The barn is 20x20 ft. The silo has a diameter of 20ft. And the distance from the barn to silo is 92 ft.

The original picture looks like this:

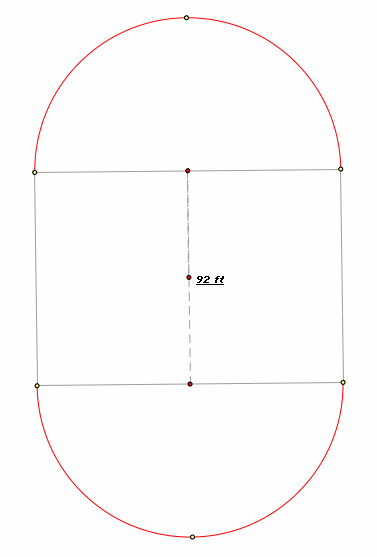
To find the area in which the goat can graze, I first though about what the area would look like if the barn and silo were not present. Without the barn and silo, it would be as if the goat was hooked to a clothesline that was 92 feet long, and the rope with which he is attached can move along the clothesline. So, there is a rectangular area that is 92 feet long and 2(76.7) = 153.4 feet wide. Then on top and below the rectangular area would be 2 semi- circles (again if the barn and silo were not there). The semi circles would have a radius of 76.7 feet. A picture of this is shown below:

So, without the barn and silo, the are of the field that the goat would be able to graze = (the area of the rectangle) + (the area of the 2 semicircles) = 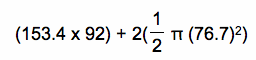= 32594.44401 feet.

However, the barn and silo are present so the actual area that the goat can graze will be less than this area because as the goat goes around the barn and silo, the rope is wrapped around these objects. It actuality, the grazing area will look something like this:

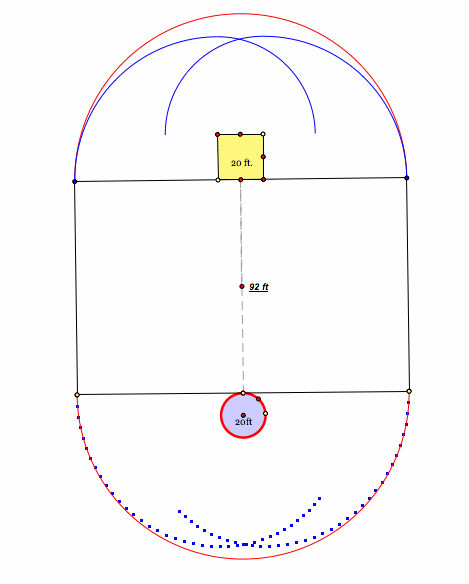
The blue lines represent the actual boundaries of the possible grazing area when taking the silo and barn into account.

Click HERE to view my GSP file of this.

and HERE to just find the trace around the silo.

To calculate the actual area for the top part (above the rectangle, and around the barn), I first subtracted the barn (20x20ft) from the original semi-circle.

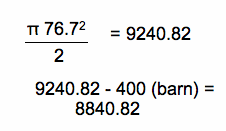
So, I know that my actual area around the barn will be less than this.

Now I need to find the area of all of the separate sectors.

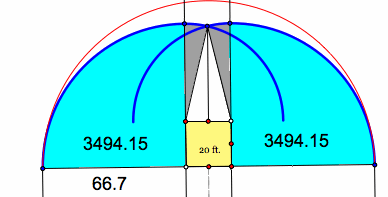
The blue sectors are each 1/4 of a circle that has a radius of 66.7 ft.

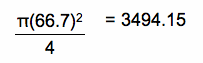
The area of the gray sectors are a little harder to find.

First, the altitude of the whole white triangle is drawn. Since it is an isosceles triangle, the altitude is also a perpendicular bisector. The sides of the left small white triangle are found to be 10, 46.7, and 45.6 ft.

Now, since the 2 little white triangles are right, we can use the cosine to find the base angles of the whole white triangle to be 77.6 degrees.

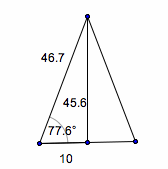
Thus, the angle in the gray sector is 90-77.6 = 12.4 deg.

So, the area of one gray sector with radius 46.7 is:

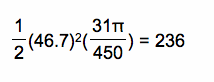
The 2 gray sectors are equal, so next I just have to find the area of the whole white triangle.

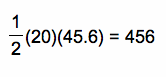
So for the area around the barn, I have 2(area of blue sector) +2(area of gray sector) + (area of big white triangle) = 2(3494.15) + 2(236) +(456) = 7916.3 ft.

7916.3 < 8840.82

Next, I need to find the actual grazing area around the silo.

Once again, the original grazing area of this part of the field would be the (area of the semi-circle) - (area of the silo) =

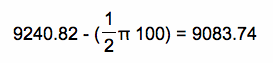
So, the actual grazing area around the silo will be less than 9083.74.

I looked at the blue trace lines and decided to try and find a circle that was close to having this arc.

In order to do this I created a secant and bisected it. Then, I found the perpendicular line through the midpoint of the secant. The center for the circle would have to be on this line.

I, then, constructed a point on this line to be the center, and I moved the point until the circle was of best fit for the arc.

The circle found is in blue.

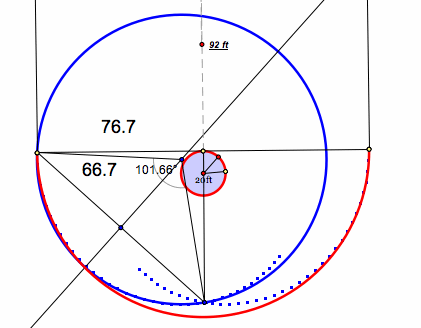
Since it is not an exact fit, the area will be an estimate.

The radius of this circle is approximately 66.7 (it is .87(76.7)).

The angle formed is 101.66 degrees.

So, the area of this sector is:

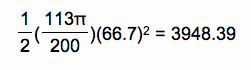
There are 2 of these so the actual area around the silo for the goat to graze is approximately 7896.78 ft.

So, the total approximate grazing area for the goat is:

(area of the rectangle) +(area around the barn) + (area around the silo) =

(14112.8) + (7916.3) + (7896.78) = 29925.88 ft