Triangle of Medians

Rozina Essani

2. If the original triangle is equilateral, then the triangle of medians is equilateral. Will an isosceles original triangle generate and isosceles triangle of medians? Will a right triangle always generate a right triangle of medians? What if the medians triangle is a right triangle? Under what conditions will the original triangle and the medians triangle both be right triangles?

---

We know that if the original triangle is equilateral, then the triangle of medians is equilateral.

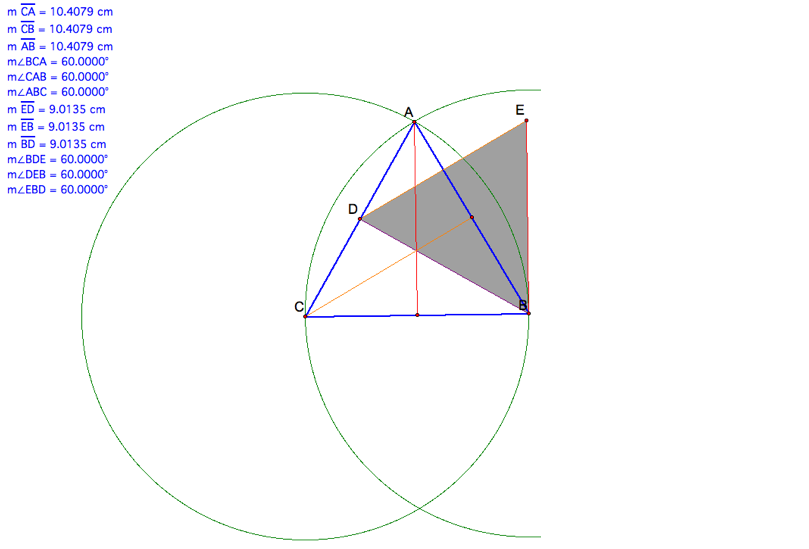
Now let us see if the same applies to an isosceles triangle.

Steps to making an isosceles triangle:

1. create a line segment of any length

2. find its midpoint

3. construct a perpendicular bisector at the midpoint

4. pick and random point on the perpendicular bisector

5. connect the vertices of the original segment to the point on the perpendicular bisector

6. to create the triangle of medians find the midpoint of AB, BC and AC, connect any one vertex with the opposite midpoint in this cast CD

7. draw parallels and D and C as shown

8. the shaded triangle is our triangle of medians

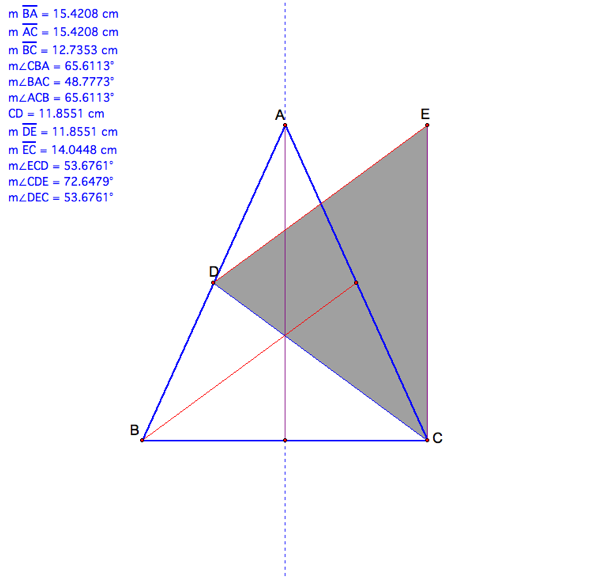
The above illustration shows that the triangle of medians of the original isosceles triangle is also an isosceles triangle, but our triangle of medians has sides CD and ED that are equal and respectively angles ECD and DEC equal. No matter what our altitude is for the original Isosceles triangle, our triangle of medians will be isosceles.

Let us now see if the same occurs for right angle triangles:

Construction of a Right Angle Triangle:

1. construct a segment of any length

2. at one end of the segment construct a perpendicular line

3. pick any point at random on the perpendicular line

4. construct line segment from the point to the vertices of the original line segment

5. do same for the construction of triangle of medians as we did with the equilateral and isosceles triangles

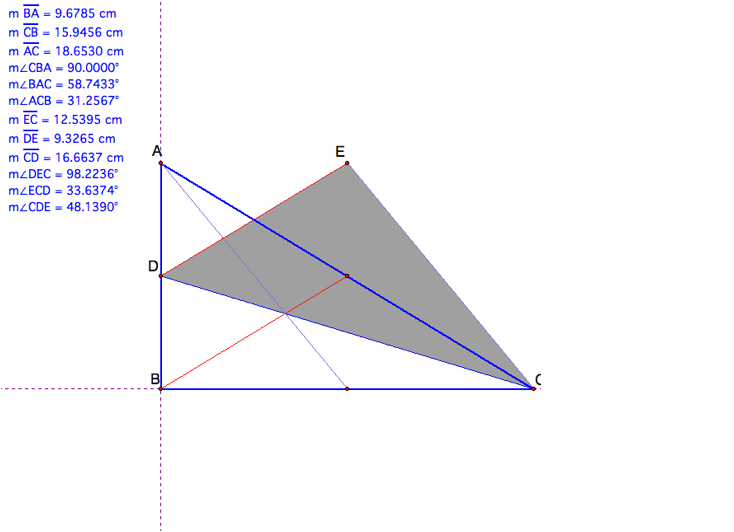
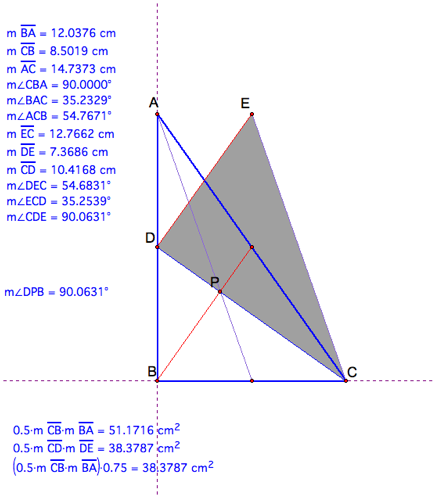
We see that the triangle of medians CDE for right triangle ABC is not a right triangle. All three angles are effected when we change the height of AB whereas when we change BC we don’t see a change in angles in CDE.

What if the medians triangle is a right angle triangle?

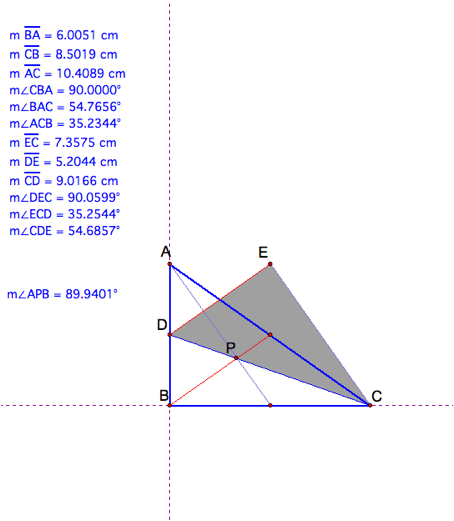
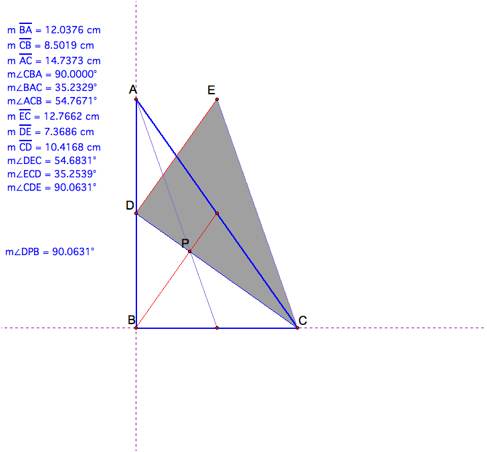
We have now made both our triangles right triangles. We see that in both cases two of our medians must be perpendicular in order to give us a right triangle of median.

We can also show that our triangle of medians is ¾th the area of the original triangle. Lets use the case of the right triangle for example.