Assignment 12:

Fibonacci Sequence

by

Margo Gonterman

The Fibonacci sequence is defined recursively as follows:

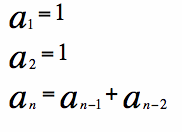
for n>2.

For example,

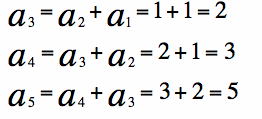
and so on.

The golden ratio, or is defined to be .

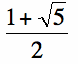For more information on the importance and history of the golden ratio, click here.

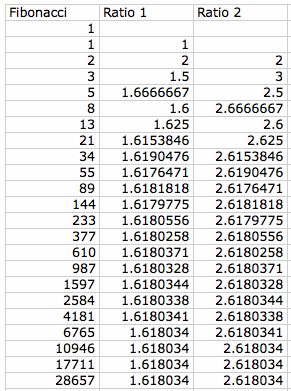
Ratio Explorations in Excel

The first column is the Fibonacci sequence.

The second column is the ratio of consecutive Fibonacci numbers.

The third column is the ratio of every second Fibonacci number.

To see the full Excel document click here.

Note that both ratios seem to converge to a particular value.

Proof of Convergence of the Ratio of Fibonacci Numbers

We want to show that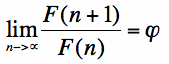and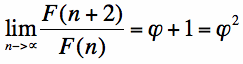

F(n+1)=F(n)+F(n-1) by the recursive definition of the Fibonacci sequence.

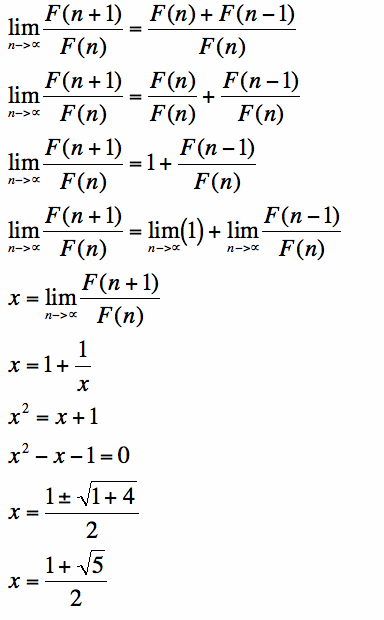
Similarly, F(n+2)=F(n+1)+F(n) by the recursive definition of the Fibonacci sequence.

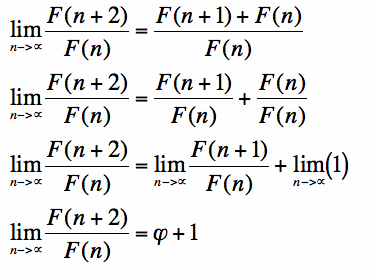
Since is the solution to, it follows that

Return