

Assignment 4:
"Prove that the three angle bisectors of the internal angles of a
triangle are concurrent."
by
Margo Gonterman
The angle bisector of an angle ABC is a ray AD such angle ABD = angle DBC.
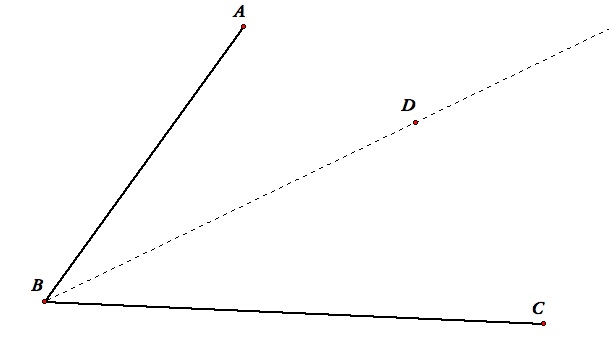
Angle Bisector Construction
- Mark a point E on the segment BC.
- Construct a circle with center B and radius BE.
- Mark the intersection of the circle with AB as point F.
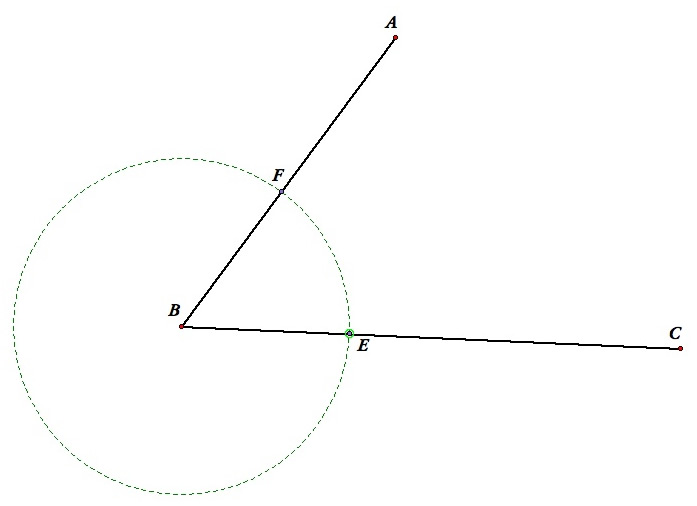
- Construct a circle with center E and radius EF.
- Construct a circle with center F and radius EF.
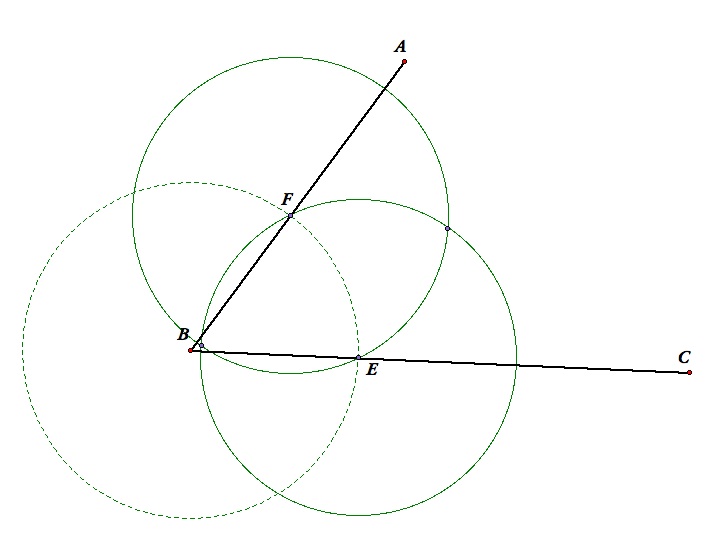
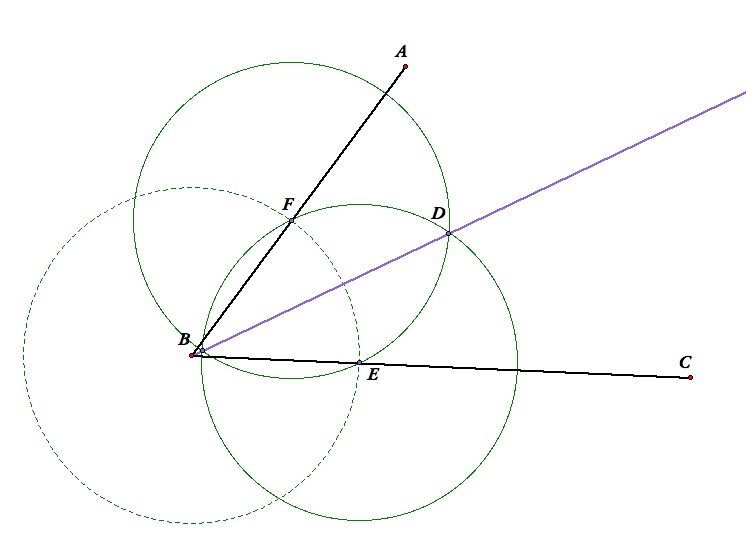
- Mark an intersection of the two circles as point D.
- Draw a ray AD.
- AD is the angle bisector of angle ABC.
Proof of Angle Bisector Construction
- Connect EF, DE, and DF.
- DF=FE since both are radii of the circle with center F.
- EF=EF since both are radii of the circle with center E.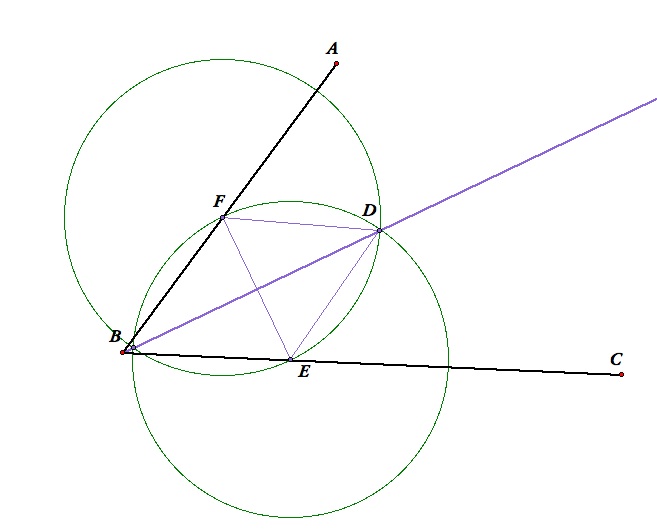
- Therefore EF=FD=DE.
- Triangle DEF is an equilateral triangle and angle DEF = angle EFD = angle FDE = 60 degrees.
- BF=BE by construction
- Thus Triangle BEF is an isosceles triangle
- Since the triangle is isosceles, angle BFE = angle BEF.
- angle BFE + angle EFD = angle BEF + angle DEF
- angle BFD = angle BED
- Then triangle BFD is congruent to triangle BED by SAS.
- Specifically, angle FBD = angle DBE
or angle ABD = angle DBC
- Thus BD is the angle bisector of angle ABC
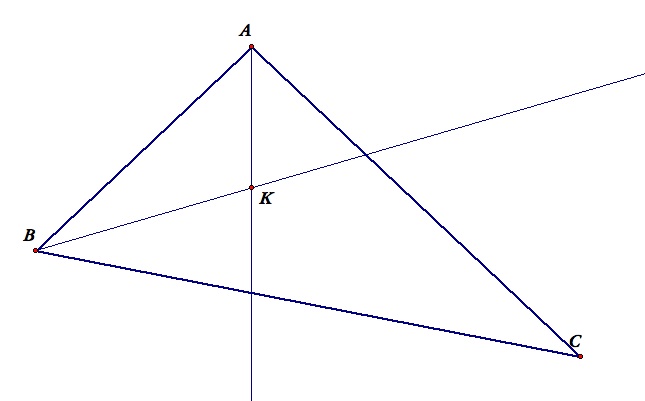
Proof of Concurrency of Angle Bisectors of a Triangle
- Given a triangle ABC, construct the angle bisectors of angle BAC and angle ABC.
- Mark the intersection of of the two rays as the point K.
- From the point K, construct segments that are perpendicular to each of the three sides of the triangle.
- Label the intersection points on side BC, AC, AB as D, E, F respectively.
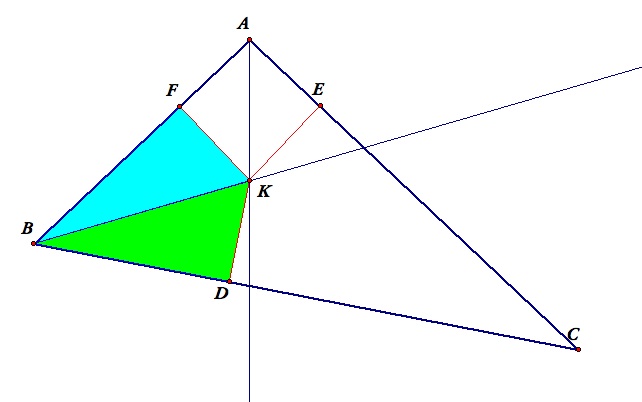
- Now consider triangle BFK and triangle BDK.
- angle BDK = angle BFK since they are both right angles.
- angle FBK = angle DBK since BK is the angle bisector.
- BK is common in both triangles.
- Therefore, triangle BDK is congruent to triangle BFK by AAS.
- Specifically, FK = DK.
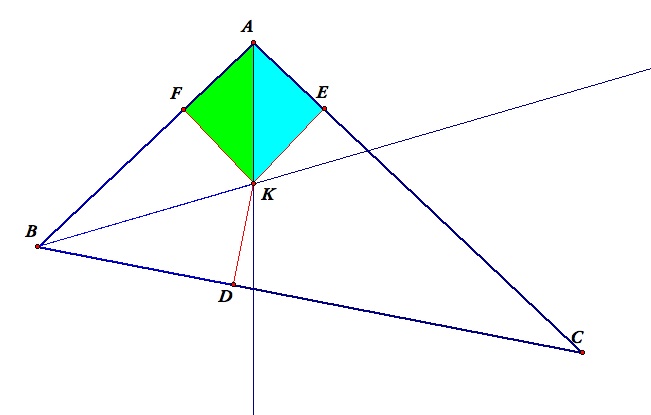
- Now consider triangle AFK and triangle AEK.
- angle AFK = angle AEK since they are both right angles.
- angle FAK = angle EAK since AK is the angle bisector.
- AK is common to both triangles.
- Therefore triangle AFK is congruent to triangle AEK by AAS.
- Specifically, FK= KE.
- FK = KE = KD.
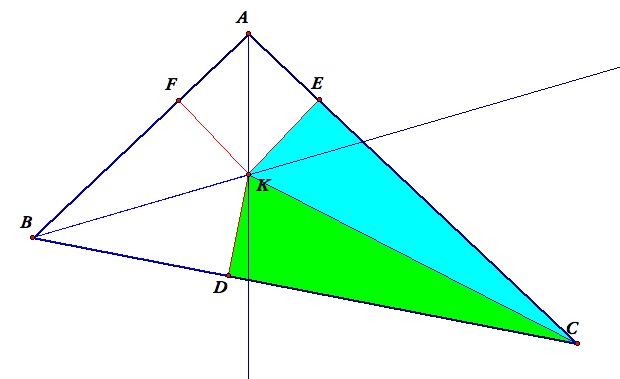
- Now, consider triangle CDK and triangle CEK.
- KE=KD
- KC is common to both triangles.
- angle KDC = angle KEC since they are both right angles.
- Then triangle CDK is congruent to triangle CEK by Hypotenuse-Side
Click here to see a proof of Hypotenuse-Side congruence
- Therefore angle DCK = angle ECK
Thus the angle bisectors of the interior angles of the triangle are concurrent.
Incenter
The point of concurrency of the angle bisectors of a triangle is the incenter of the triangle.
Click here to see a GSP sketch of the incenter.