

Assignment 6:
"Parabola Construction"
by
Margo Gonterman
A parabola is the set of all points that are the same distance from a line, called the directrix, and a point, called the focus.
Parabola Construction
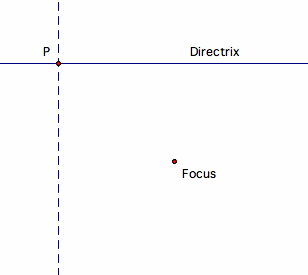
- Construct a line that will be the directrix
- Construct a point not on the line to be the focus
- Construct a free point P on the directrix
- Construct a line through P that is perpendicular to the directrix
- Connect P and the focus.
- Construct the perpendicular bisector of the line connecting P and the focus through the midpoint M.
- Mark the intersection of the perpendicular bisector and the line perpendicular to the directrix through P as X.
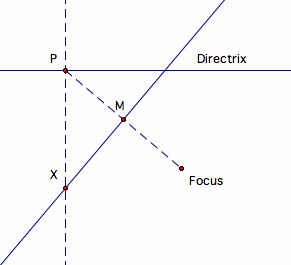
-X will trace the parabola as P moves along the directrix
- Line XM is the line tangent to the parabola
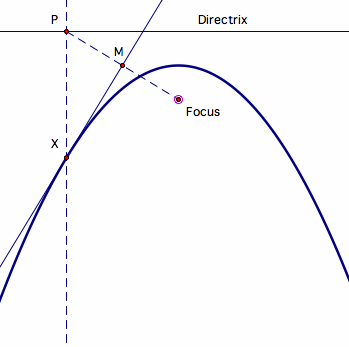
Proof that Construction Satisfies Definition
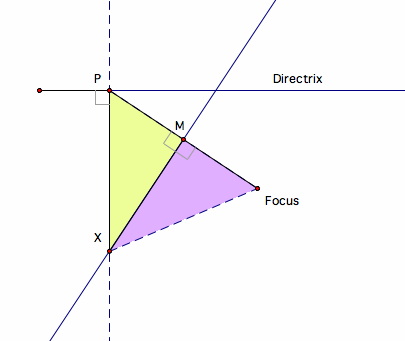
- Consider triangle PMX and triangle FMX.
- Segment XM is common to both triangles.
- Line XM is the perpendicular bisector of line PF.
Therefore:
PM=FM
Angle PMX=Angle FMX since they are both right angles
- By SAS (side-angle-side), the two triangle are congruent.
Specifically, segment PX=segment FX
- PX is the distance between X and the directrix.
- FX is the distance between X and the focus.
Therefore the point X is equidistant from the focus and the directrix.
GSP Sketches
Click HERE to see a GSP sketch of the construction of a parabola. The point X will trace as it is animated.
Click HERE to see a GSP sketch of the construction of a parabola. The tangent line will trace as it is animated.
Extensions
What happens when the directrix is not a line?
Click HERE to see what happens when the directrix is a circle and the focus is inside the circle.
Click HERE to see what happens when the directrix is a circle and the focus is outside the circle.