

Assignment 8:
"Exploring Orthocenters"
by
Margo Gonterman
The orthocenter of a triangle is the point located at the intersection of all three altitudes of the triangle.
If the triangle is acute, then the orthocenter will fall inside the triangle.
If the triangle is obtuse, then the orthocenter will fall outside the triangle.
If the triangle is right, then the orthocenter will lie on the vertex with the right angle.
This exploration will focus on acute triangles.
Prove that 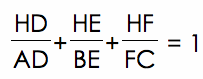
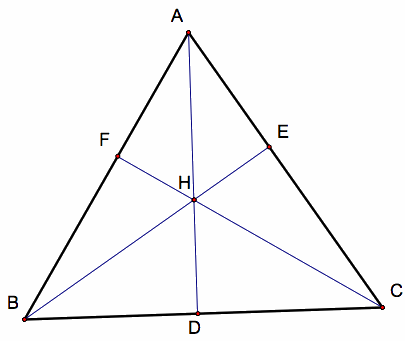
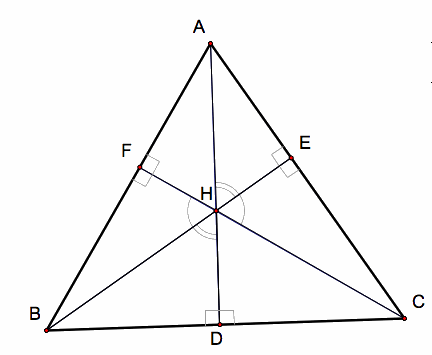
The altitudes divide the triangle into six smaller right triangles.
Vertical angles give the similarities listed below.
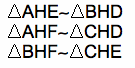
These similarities are illustrated in the image below.
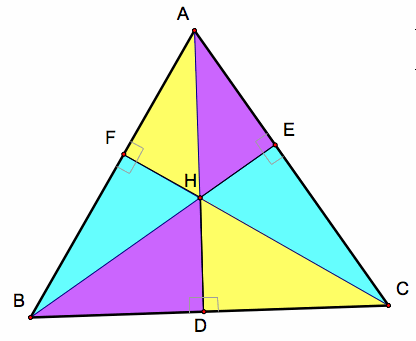
To prove the desired relationships, consider the three areas illustrated below.
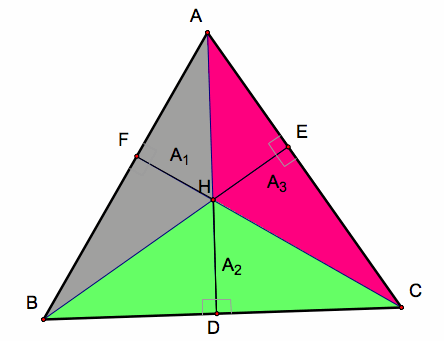
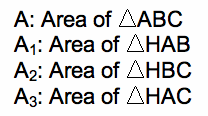
Below are the calculations for the area of the three triangles above plus the area of the entire triangle ABC.
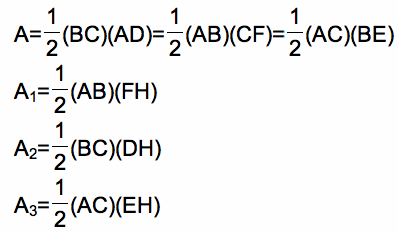
The entire triangle ABC is equal to the sum of the three smaller triangles.
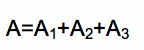
Dividing the above equation by A yields the following.
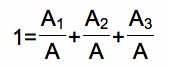
Substituting the equivalent areas into this equation yields the following:
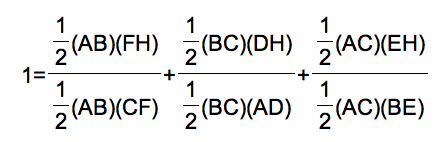
Simplifying this equation yields the desired relationship.
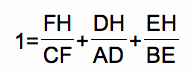
Prove 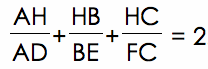

The relationships below come from the altitudes of the above triangle.
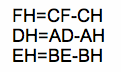
Using the result of the previous proof, plug in the values from above.
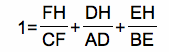
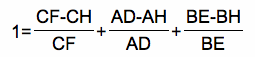
Rewriting and simplifying yields the following.
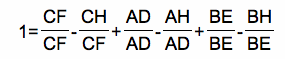
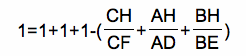
Solving for the desired ratios yields the desired relationship.
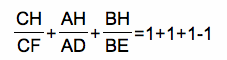
![]()