Assignment 9:
"Pedal Triangles"
by
Margo Gonterman
The pedal point can be any point either inside the triangle or outside the triangle.
The pedal triangle has vertices that are the feet of the perpendiculars from the pedal point to each of the sides of the original triangle.
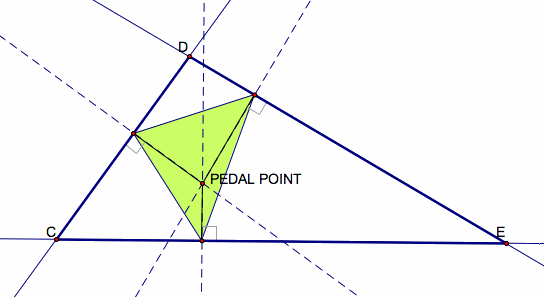
See below for an example of a pedal triangle when the pedal point is inside the triangle.
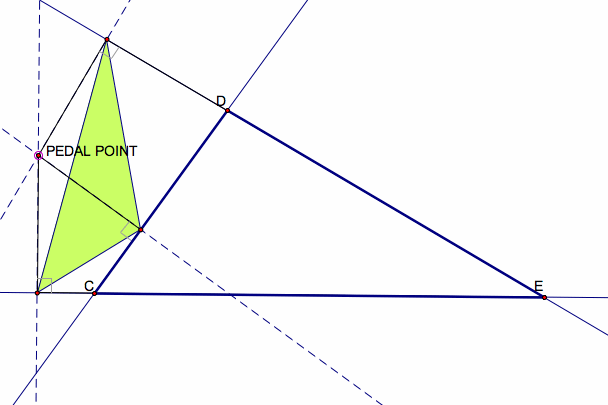
Below is an example of a pedal triangle that is completely outside the original triangle.
What if the pedal point is on the vertex of the triangle?
When the pedal point is on a vertex of the original triangle, the pedal triangle degenerates into the altitude of the original triangle.
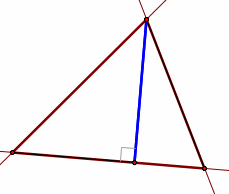
When the triangle is acute, the pedal triangle (altitude) is inside the original triangle.
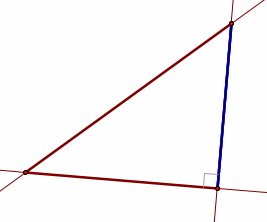
When the triangle is right, the pedal triangle (altitude) lies along one of the side of the original triangle.
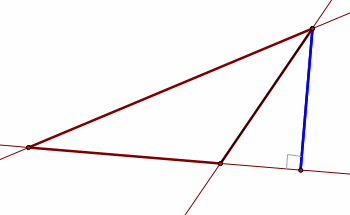
When the triangle is obtuse, the pedal triangle (altitude) lies outside the original triangle.
What if the pedal point is the centroid of the triangle?
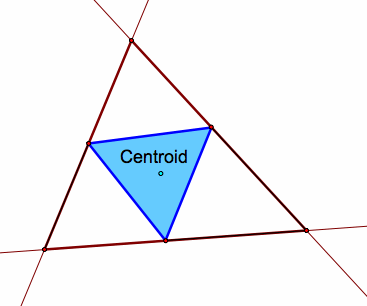
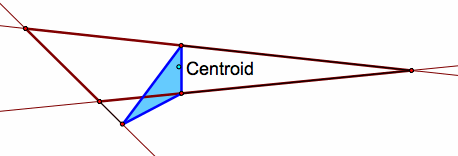
Note that when the pedal point is the centroid of the triangle, the pedal triangle is never completely outside the original triangle.
What if the pedal point is the orthocenter of the triangle?
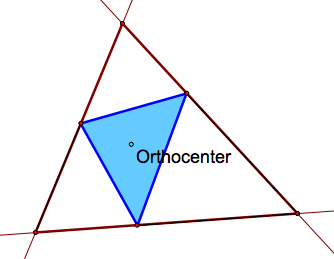
Note that when the triangle is acute, the orthocenter and the pedal triangle lie inside the original triangle.
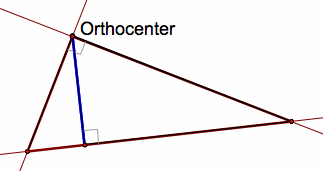
Note that when the original triangle is a right triangle, the orthocenter lies at the vertex with the right angle and the pedal triangle degenerates to the altitude from that vertex.
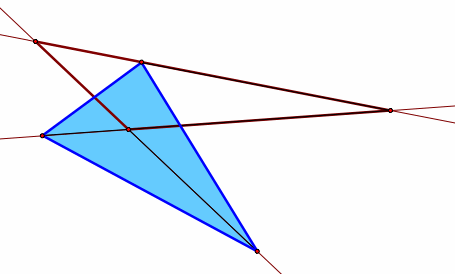
Note that when the original triangle is obtuse, the orthocenter lies outside the triangle and the pedal triangle lies partially outside of the original triangle and contains the obtuse angle.
What if the pedal point is the incenter of the triangle?
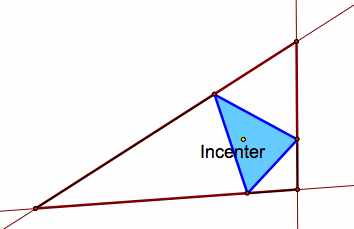
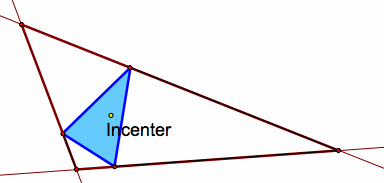
Note that when the pedal point is the incenter of the triangle, the pedal triangle is always completely inside the original triangle.
What if the pedal point is on the incircle of the triangle?
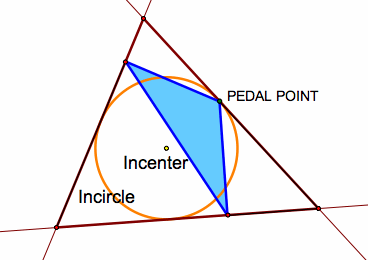
Click HERE to see an animate of the pedal triangle as the pedal point rotates around the incircle.
Notice that the pedal triangle is always inside the original triangle.
What if the pedal point is the circumcenter of the triangle?
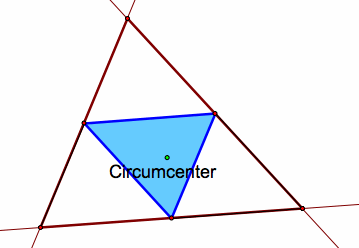
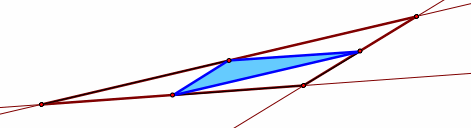
Since the circumcenter is the intersection of the perpendicular bisectors of the sides of the original triangle, the pedal triangle is the triangle formed by connecting the midpoints of the sides of the original triangle. Thus, when the pedal point is the circumcenter of the triangle, the pedal triangle is always completely inside the original triangle.
Note that the circumcenter is not always contained in the pedal triangle.
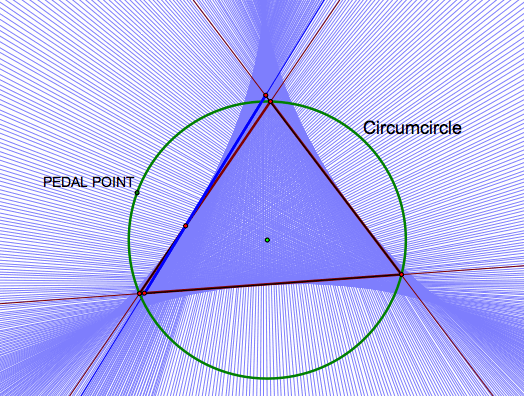
What if the pedal point is on the circumcircle of the triangle?
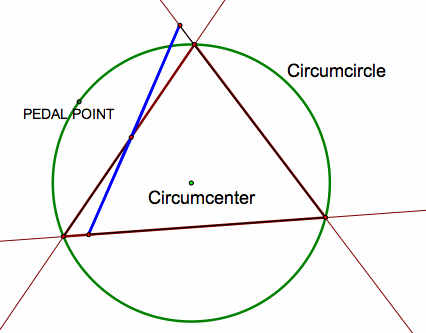
When the pedal point is on the circumcircle of the original triangle the pedal triangle degenerates into a line segment. This line is called the Simson Line.
Click HERE to see an animate of the pedal triangle as the pedal point rotates around the circumcircle.
Some Interesting Properties of the Simson Line
Tracing the midpoint of the Simson Segment gives an ellipse.
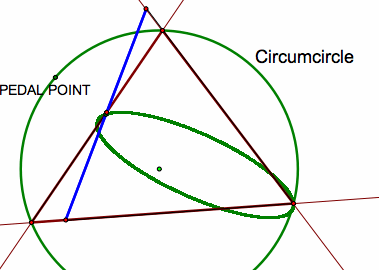
Tracing the Simson line as the pedal point rotates around the circumcircle gives a deltoid.