by
SOMIN KIM
Examine graphs for the parabola 
for different values of coefficients.
Fix two of the vales for a, b, and c.
(Make at least 5 graphs on the same axes as you vary the third value.)
1. I will fix a and b, then change value of c.
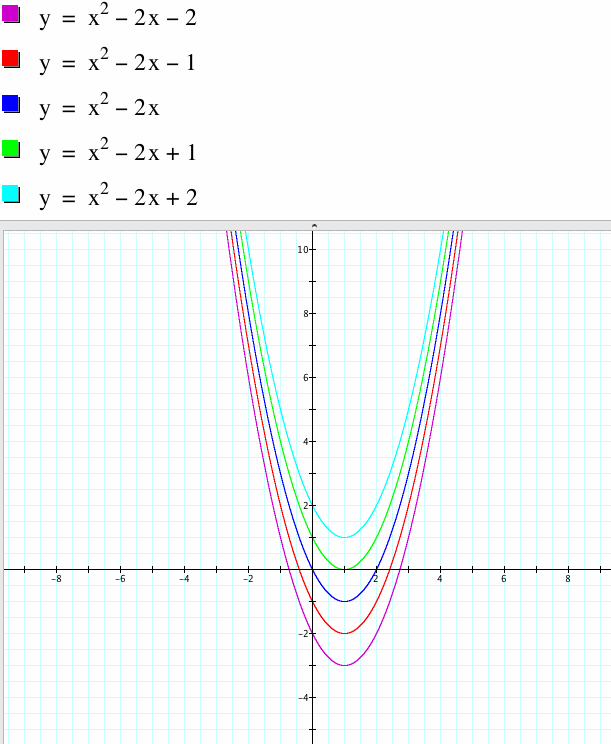
The graphs are moved by value of c. Value of c decides the graph's y-intercept.
2. I will fix b and c, then change value of a.
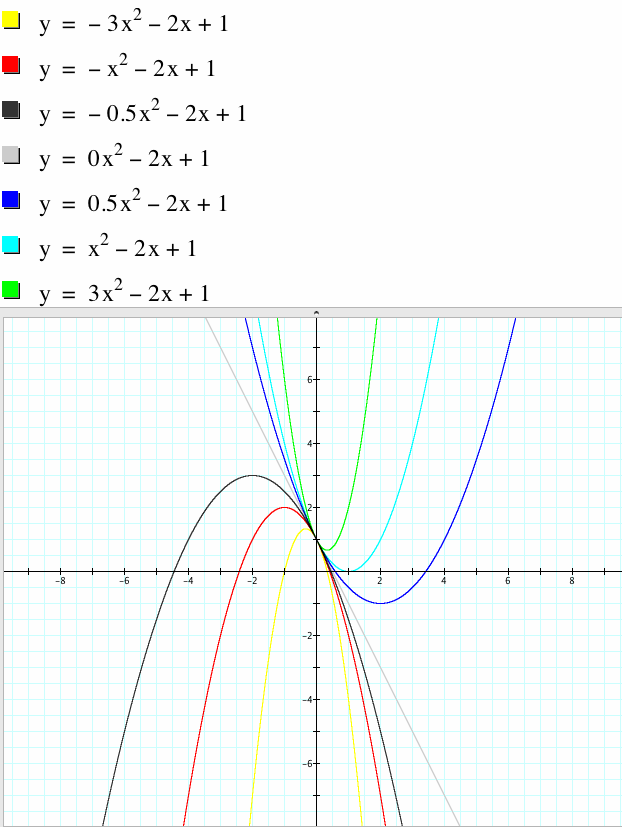
Because value of c which decides y-intercept is fixed as 1, all graphs are meet (0,1).
If value of a is changed, the curve of graphs is changed.
When the value of a is positive integer, the graph is concave.
When the value of a is negative integer, the graph is convex.
As 
is getting bigger, the slope of graph is steep.
If a=0, the equation becomes a linear equation.
3. I will fix a and c, then change value of b.
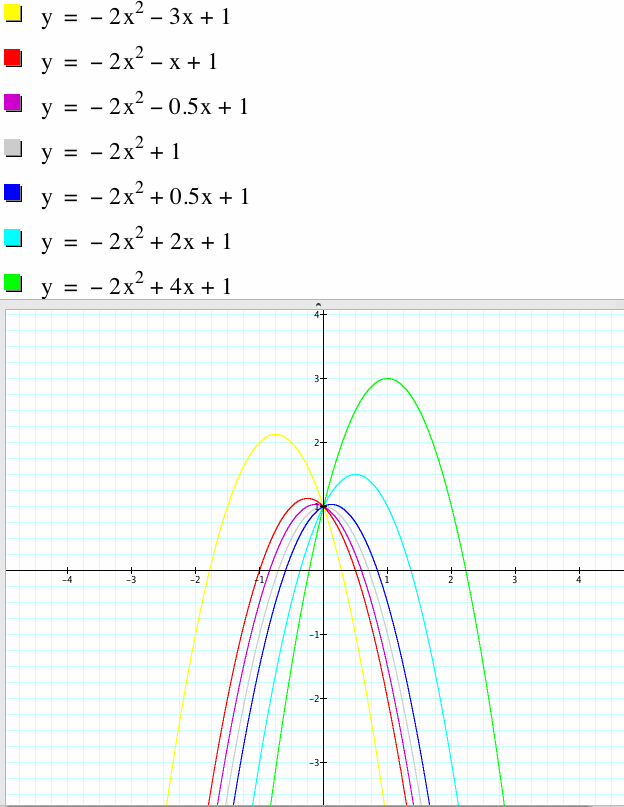
Because value of c which decides y-intercept is fixed as 1, all graphs are meet (0,1).
If value of b is changed, an apex of graphs is changed.
When the value of b is positive integer, an apex of graph is on quadrant I.
When the value of b is negative integer, an apex of graph is on quadrant II.
If b=0, an apex of graph is on y-axis.