---

SOMIN KIM

---

Graphs in the xa plane.

Consider the equation

Now graph this relation in the xa plne. We get the following graph.

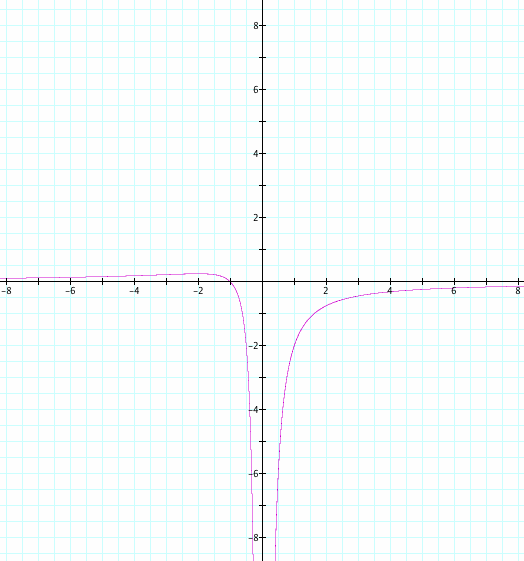
If we take any particular value of a, say a = - 3, we can add a line parallel to the x-axis. In addition, a parallel line will intersect with the original graph, and the intersection points correspond to the roots of the original equation for that value of a. We have the following graph.

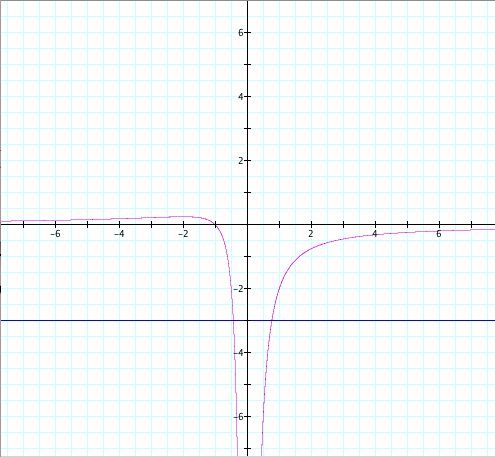
For each value of a we select, we get a horizontal line. It is clear on a single graph that we get no real roots of the original equation when a > 0.25, one negative real root when a = 0.25 and a = 0, two negative real roots when 0 < a < 0.25, one negative and one positive roots when a < 0.

Consider the case when c = - 1 rather than + 1.

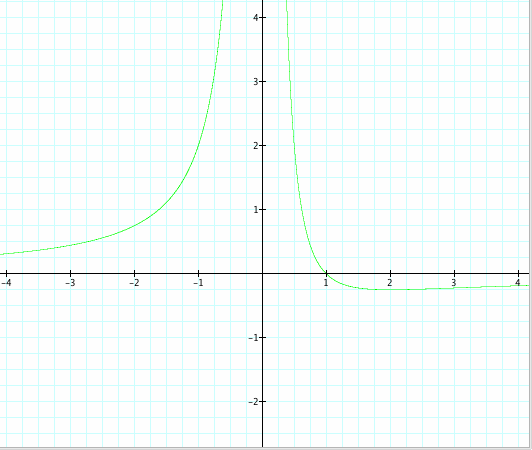
When I graph other values of c on the same axes, the graphs are expressed like these.

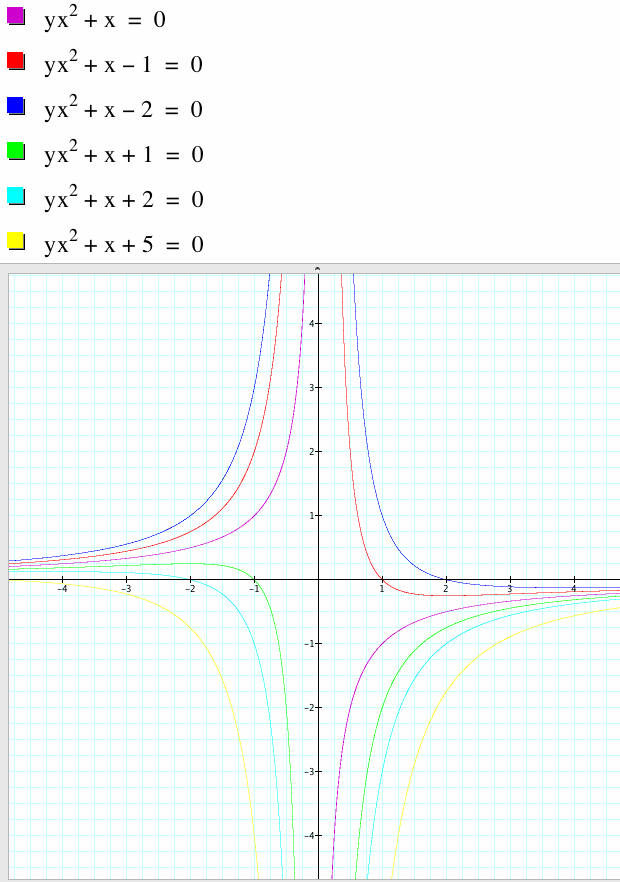
When c = 0, it becomes a graph of , and it is on quadrant II and IV. When c < 0, graph is on quadrant I, II, and IV. when c > 0, graph is on quadrant II, III, and IV.