---

By

SOMIN KIM

First, there are two type of Tangent Circle, when two circles are given.

Case1. the tangent circle goes around, connecting a large circle and connecting external surface of tangent circle with a small circle.

Case2. the tangent circle goes around, connecting a large circle and connecting internal surface of tangent circle with a small circle.

Case 1. ----------------------------------------------------------------- Case 2. --------------------------------------------------------

To view and use my script tool for case 1. click here, or for case 2. click here.

Each one case can be divided into three cases by the location of two given circles.

There are three cases for case1.

Case1-1: One given circle lies fully inside the other. To view the locus of the center of case1-1 click here.

Case1-2: The 2 given circles intersect one another. To view the locus of the center of case1-2 click here.

Case1-3: The 2 given circles form completely disjoint circular regions. To view the locus of the center of case1-3 click here.

There are three cases for case2.

Case2-1: One given circle lies fully inside the other. To view the locus of the center of case2-1 click here.

Case2-2: The 2 given circles intersect one another. To view the locus of the center of case2-2 click here.

Case2-3: The 2 given circles form completely disjoint circular regions. To view the locus of the center of case2-3 click here.

In these investigations, I realized that all 6 cases either an ellipse or a hyperbola is formed.

The ellipse appears at case1-1, 1-2, and case2-1. The hyperbola appears at case1-3,case2-2, and case2-3.

If you look carefuly, you can find a feature of locus at case 1-1.

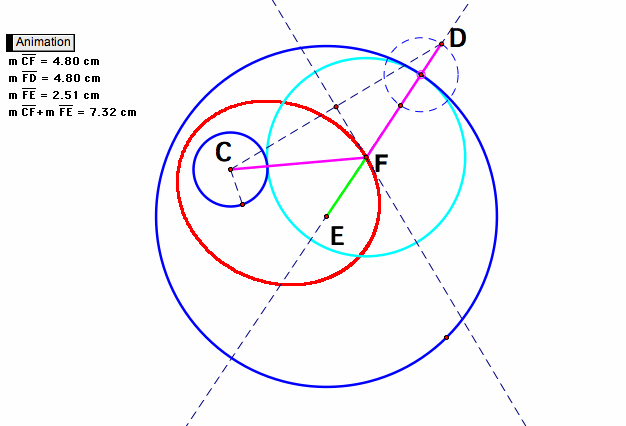
You can see sum of the length of CF and FE is fixed no matter where the point F is on the ellipse.

To view this as a GSP file click here.

Since CF+EF=DF+EF, and DF+EF is not changed, CF+EF is fixed.

Therefore, loci of points F such that CF+EF is fixed form ellipse, and we call C and E the foci of ellipse.