Polygonal Spiral

In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.

In the real world, there are many spirals such as the pattern on the nautilus shell, the galaxy and, the typoon . We can make the spirals using the regular polygons.

In the following discussion, we will make the specific polygonal spirals such as a regular triangle, a square, and a regular pentagon with unit side. In addition, we will figure out how we find the n-polygonal spirals.

There are polygonal spirals.

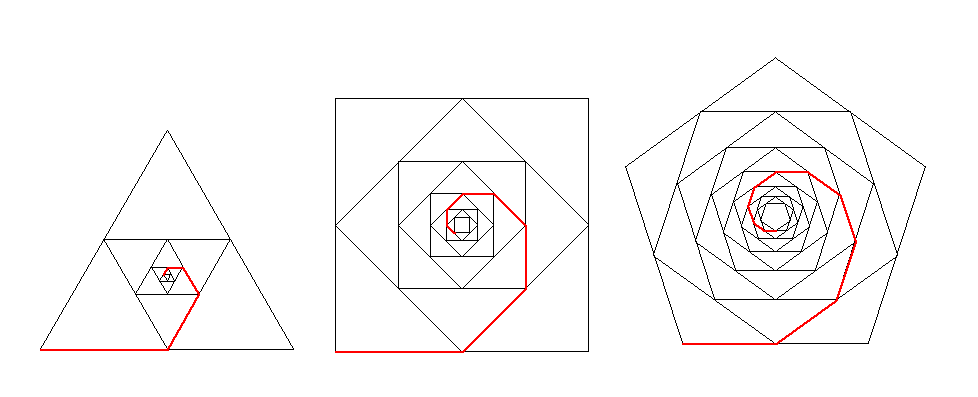
Let's make a regular triange spiral.

we construct the midpoints of a equilateral triangle of length 1 and then connect the midpoints to form another equilateral triangle. In repeating this process, a sequence of concentric triangles are generated connected at the midpoint of the outer triangle. If we draw the line from the first triangle's corner to the intersection of its midpoint and the second triangle and repeat this process, we can find the spiral. The spiral is highlighted in red in the following sketch.

In addition, we can get the length of this spiral, and find generalization of the total length of polygonal spiral.

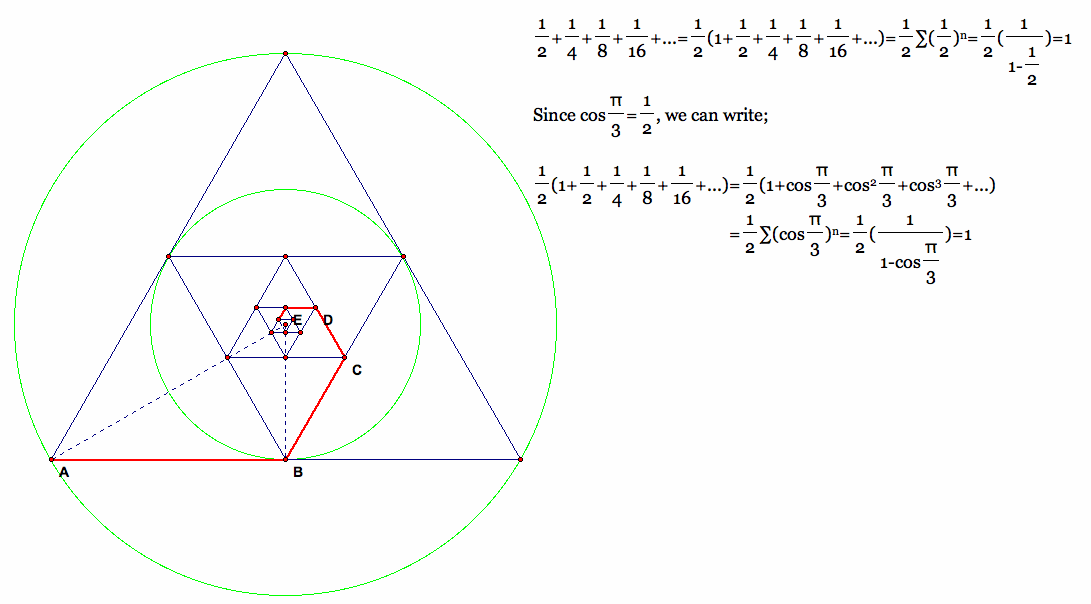
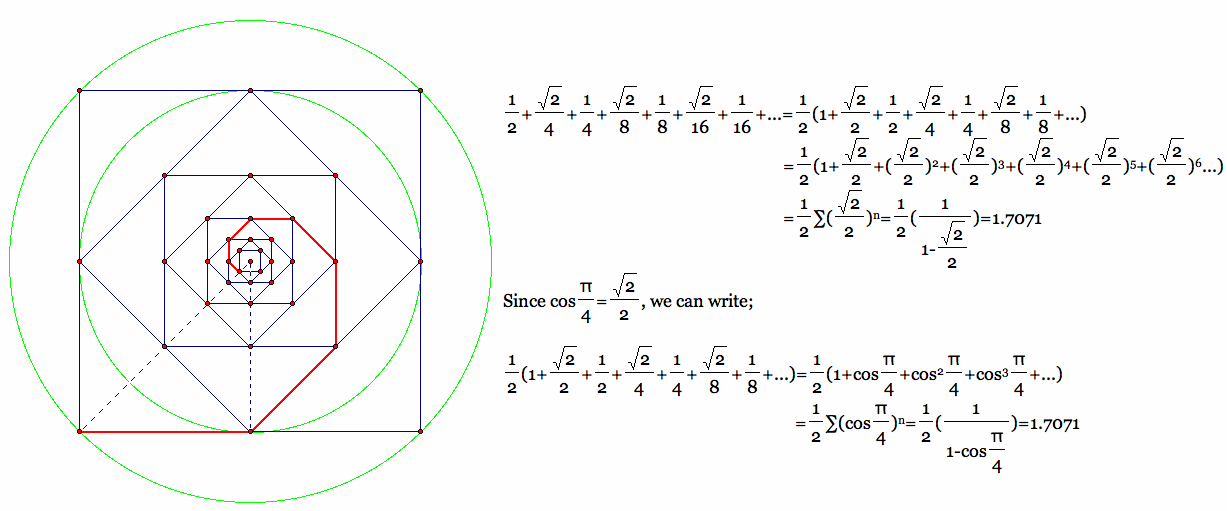
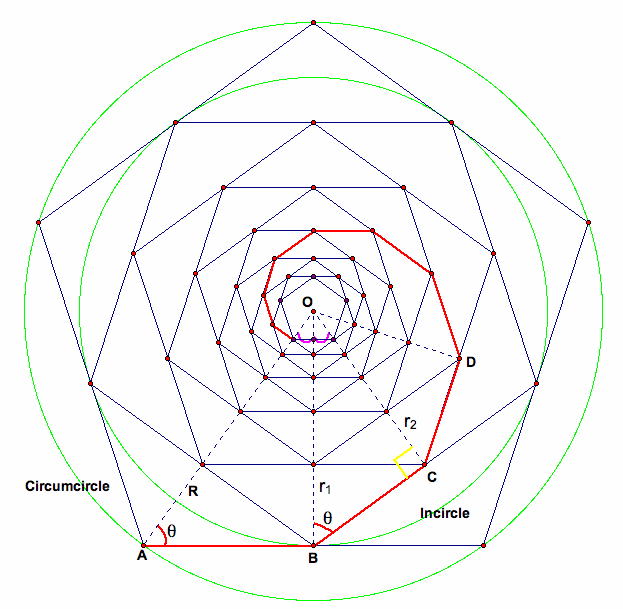
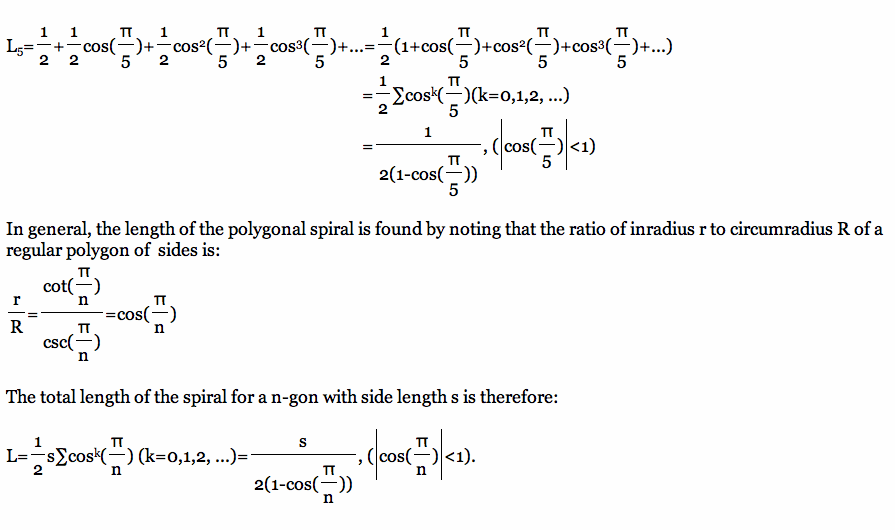
There are traces of polygonal spiral points starting from each corner of a square. It seems the mice problem, also called the beetle problem (n mice start at the corners of a regular n-gon of unit side length, each heading towards its closest neighboring mouse in a counterclockwise direction at constant speed. The mice each trace out a logarithmic spiral, meet in the center of the polygon, and travel a distance

).

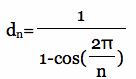However, in the animation I made the point each trace out a polygonal spiral.

If you want to see GSP file, CLICK HERE.