Quadratics in the XC plane

Kasey Nored

Our parent quadratic makes our familiar parabola.

y = ax² + bx + c where b and c equal zero

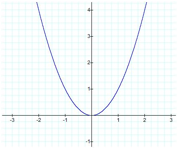
The manipulation of a, b, and c shifts and dilates our parabola.

This write-up intends to explore the xc plane where c serves as y, for example to graph a point in the xc plane (x, c) would be the coordinates. When we manipulate our quadratic ax² + bx + c, using 1 for a and b, and solve for c we find that c = –x² – x

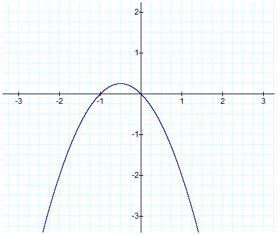
Our xc plane appears to merely flip and shift our parent function, with our vertex at

When we change our original value of c to 5, the red graph, or to .25, the black graph, our parabola dilates but also moves our vertex.

For the equation our vertex lies at and the graph still has zeros at 0 and -1 which is reasonable

as our zeros are linked with our values of a and b and here we have not changed our a and b values.

For the equation our zeros remain and our vertex lies at

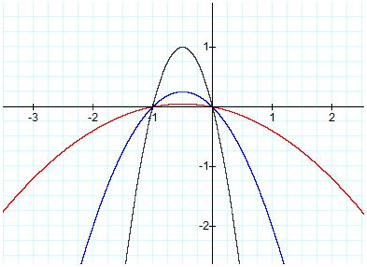
If we animate the denominator for values between -10 and 10 we see the graph below.

You notice that the graph continues to have the original zeros and dilates while changing the vertex.

Also of interest is the point where c = 0 the graph is undefined as dividing by zero is undefined.