Centers of Circles

Kasey Nored

This write-up is an exploration targeted for high school students.

Centroid

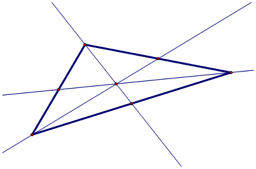
A centroid of a triangle is the common intersection of the three medians of the triangle. The median is constructed by finding the midpoint of a side of a triangle and connecting the opposite vertex to the midpoint. A centroid will remain inside the circle for the three types of triangles categorized by their angles.

Acute Triangle

Right Triangle

Acute Triangle

Obtuse Triangle

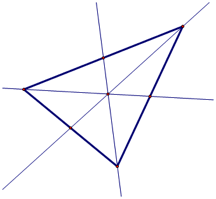
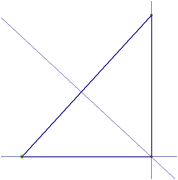
Orthocenter

Orthocenters are found by the intersection of the altitudes of a triangle. Altitudes are found by creating a line perpendicular to the line containing the side of the triangle that crosses through the opposite vertex. You will notice that orthocenters, unlike centriods, can be inside, on or outside the triangle.

Right Triangle

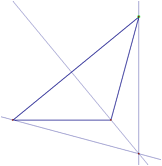
Obtuse Triangle

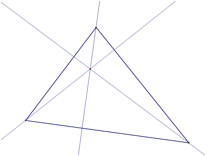
Acute Triangle

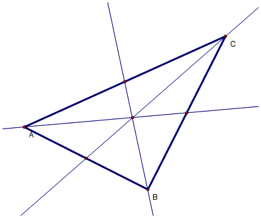
Circumcenter

Circumcenters are found at the intersection of the perpendicular bisectors of the sides of the triangle. The perpendicular bisector is created by bisecting each side of the triangle with a perpendicular line. A circumcenter is also the center of a circle, which passes through each of the three vertices of the triangle.

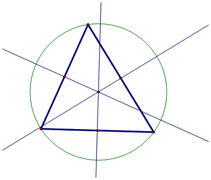
Acute Triangle

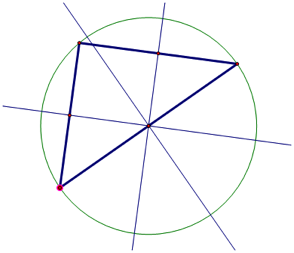
Right Triangle

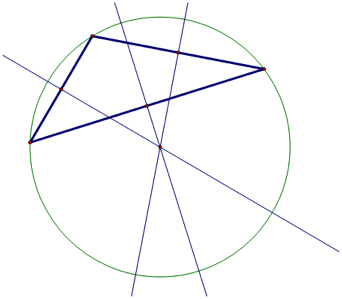
Obtuse Triangle

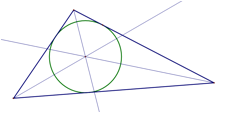
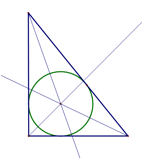
Incenter

An incenter is found at the intersection of the angle bisectors of a triangle. The incenter is the center of the incircle, an inscribed circle of the triangle.

Right Triangle

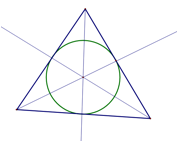
Acute Triangle

Obtuse Triangle