Problems

by

Kasey Nored

Our problem is given points A, B and C, draw a line XY such that AX = XY = YC

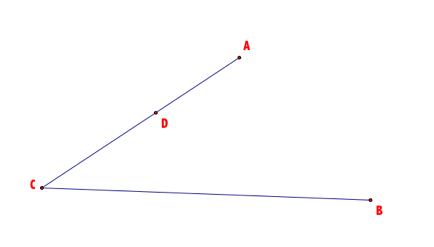
First we pick an arbitrary point, let’s say D.

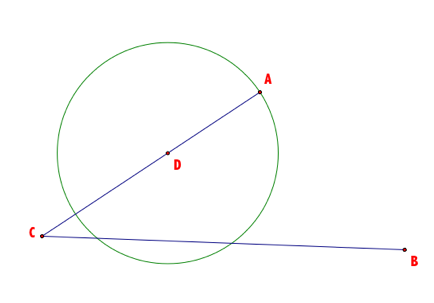
Draw a circle with its center at D and radius DA.

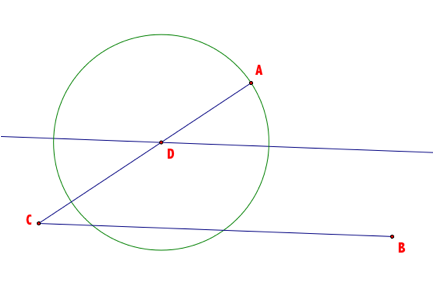
Construct a parallel line through D being parallel to CB.

Construct the intersection of our parallel line and our circle, E and our circle and the segment CB, F.

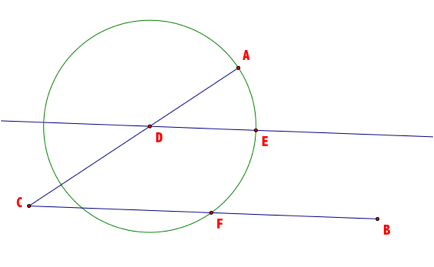
Construct the segment DF and a line parallel to DF through E. We now have constructed a rhombus DEGF.

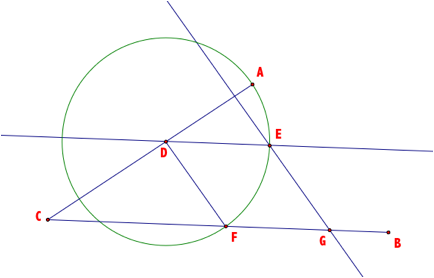
Constructing Circle F and Circle G provides a better visual that DEGF is actually a rhombus.

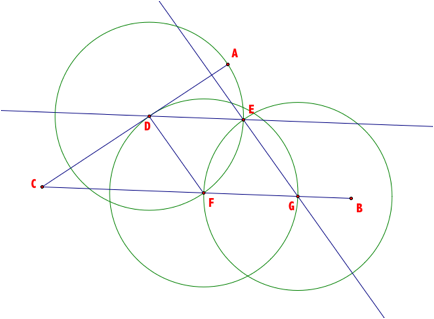
We can translate our original rhombus to find the points X and Y that meets our original conditions.

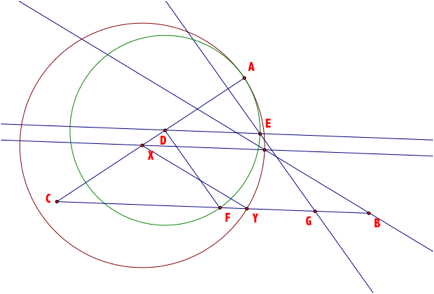
This is a bit messy, if we hide Rhombus DEGF we can begin to see that our Rhombus that meets the conditions of the problem. Construction of Circle Y assists in the visual.

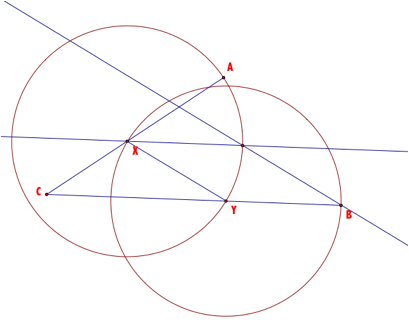
The segment AX is a radius of circle X, segment XY is a radius of circle X and Y. Segment YB is a radius of circle Y. AX = XY = YB.