Altitudes and Orthocenters

by Kasey Nored

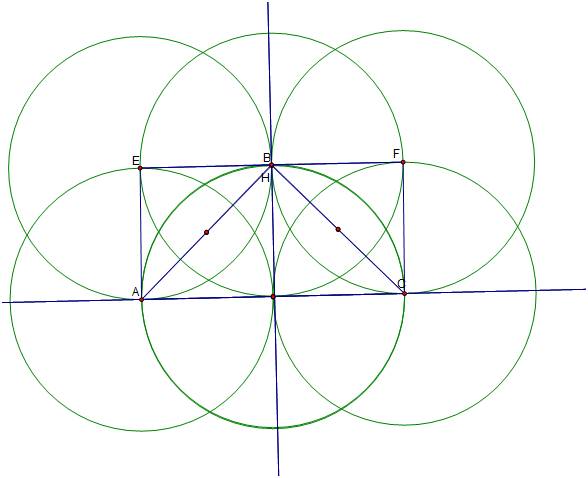
We constructed a triangle ABC with the Orthocenter H, then constructed the Orthocenter of triangle HBC and the Orthocenter of triangle HAB, and Orthocenter of triangle HAC. We also constructed the Circumcircles of triangles ABC, HBC, HAB, and HAC. The image is below.

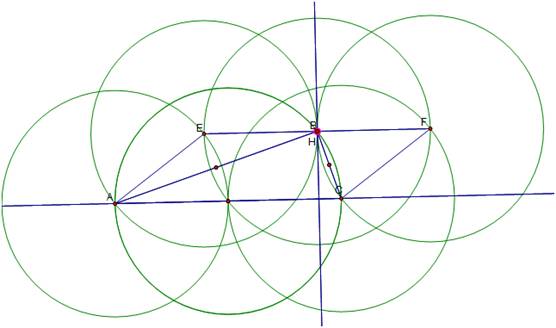
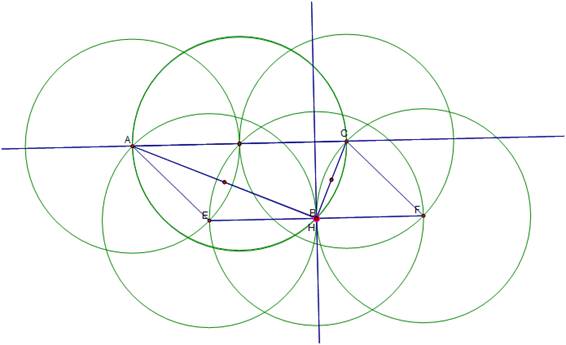
To futher explore we move a vertex of ABC to H and investigate the result.

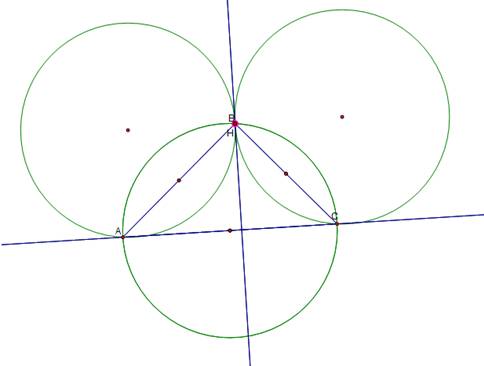
Our four circumcircles become three regardless of which vertex is translated to H.

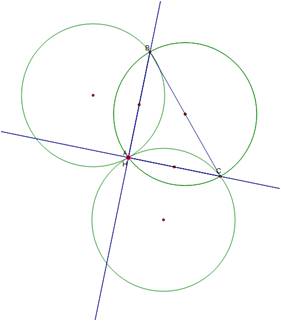
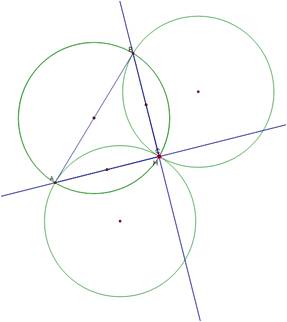
The circumcircle of ABC overlaps the circumcircle of H and the two vertices of the triangle which are opposite the vertex H has been translated to; which seems reasonable as we are translating H to overlap the original triangle.

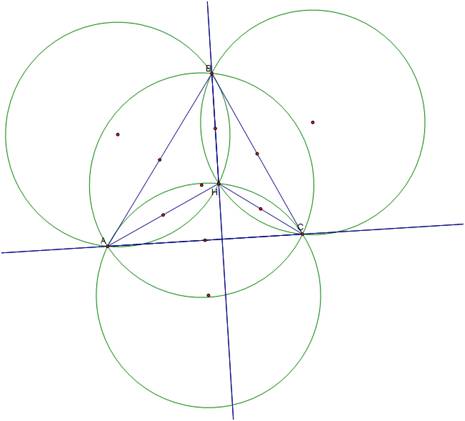
Our new circles all have equal radii and that distance is equal to the distance of the Median of the new triangle ABC.

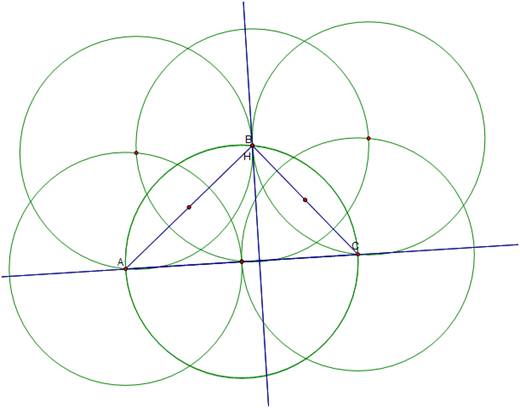
If we label the points where the circles intersect which the center of the circumcircles of triangles AHB and CHB, E and F and draw segments between the centers of the circles a parallelogram is formed regardless of how we shift the triangle ABC.